The "Yin Yang Fire" algorithm
Contents
1. The historical background
2. The Yin Yang Fire algorithm
3. Scientific aspects
4. Things to try
1. The historical background
The control of fire by early humans was a turning point of the human evolution and it started approximately 125,000 years ago and earlier.
Then, later on in the 1980s, there was a period where fire-simulations based on cellular automaton where very popular, because CPU-Power was rare and expensive.
The simplest fire algorithm looks like this (as seen on youtube here):

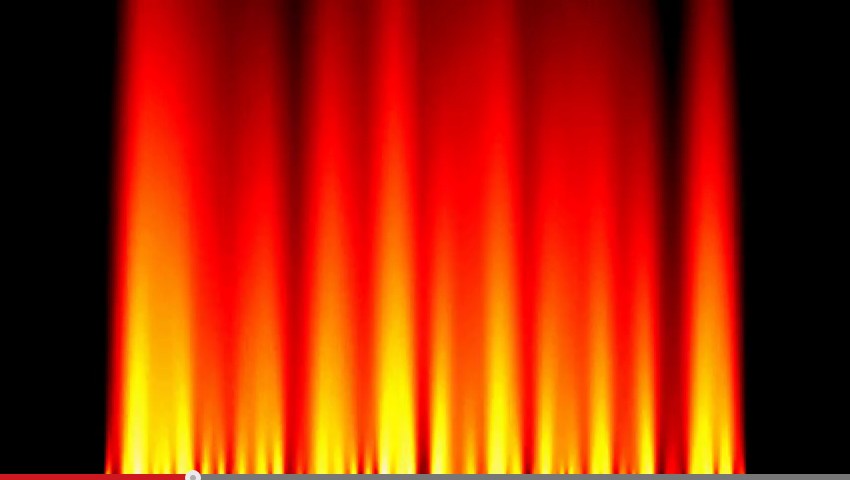
It's a 1D-CA that uses the average value of the three cell below it to create a new value. The fire itself is "feed" by the buttom line with constantly new random values for every step of the calculation of the matrix.
A more advanced version to simulate fire with CA is this algorithm:

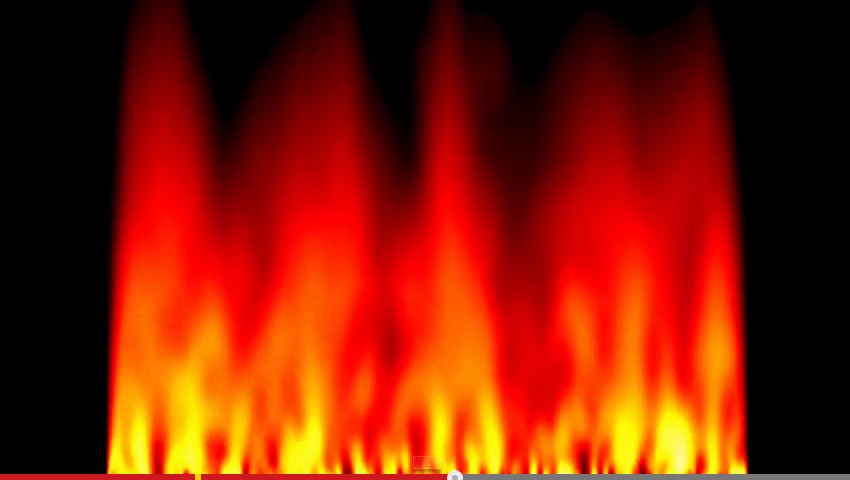
It's using the three cells from below plus the previous value of the cell that is updated, and it's looking quite a bit more realistic. It's now a 1D CA with memory (somewhat inbetween of a 1D and 2D CA).
2. The Yin Yang Fire algorithm
Jack Ruijs
In the 1990s Jack Ruijs tried to create a kind of 2D totalistic CA fire algorithm out of the normal "1,5D" CA (see here). He came up with an algorithm, that has the functions of the diffusion (the fading out) of the fire, as well as the possibility to start a new fire before all values decrease to zero. And once a fire is started, the surrounding cells can also increase their values.
So in addition to a "normal" fire, that only fades out going upwards, the algorithm can also make the opposite, and do a kind of "ignition" and a spread out by itself. So a fire that is doing what a fire does but also it's inversion, can be surely called a "yin yang fire".

It uses a Moore-Neighborhood plus the central cell. The average of this nine cells then leads to the new value of the center cell because the centre cell adapts to it's surrounding and increases or decreases it's new value. But if the value of the surrounding decreases to a certain limit, the new value is not an adaption to the average, but it becomes the highest possible value. This starts a new "ignition" in the update-cycle.
And this is how it looks like (created with the freeware programm "Visions Of Chaos"):
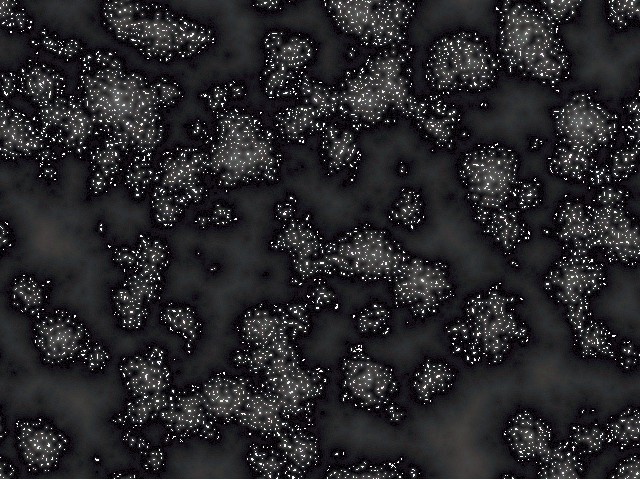
The algorithm itself
Because of the fact, that Jack Ruijs kept the algorithm as a secret, it had to be rediscovered by Mack Tuesday in the year 2015. He used reverse engineering and his algorithm looks like this (in pseudocode):
if the old value of the centre cell times nine >= the cell sum of all 9 cells (Moore plus centre cell)
then reduce the value of the centre cell with the operation minus one
if the old value of the centre cell times nine < the cell sum of all 9 cells
then increase the value of the centre cell with the operation plus one
but if the value of the centre cell < 0
then replace the old value with the maximum value (depending on the number of used states)
So this algorithm can somewhat adapt positively and negatively to its surrounding, and it can also start a fire with new sparkles in the cells, that drop below zero.
Mathematically it looks like this:
if (centre cell * 9 + 2) >= sum of all 9 cells; then new value = old value -1; else new value = old value +1
but if the new value of centre cell < 0, than new value = 63 (if you use 64 states ranging from 0-63)
The original algorithm, that was equivalent to the reinventend one by Tuesday, may have looked like this:
if (Cell 1 + Cell 2 + Cell 3 + ... Cell 9) / 9 - 2/9 <= value of the centre cell; then new value = old value - 1; else new value = old value +1
but if ... (see above)
What the algorithm does is to adapt the value of the centre cell to the average value of the environment plus a damping factor (just like the old fire algorithms). But if the average value of the surrounding is higher, it uses a amplification factor (a kind of negative damping). And if the value drops below zero, there is a new ignition of the fire, so the value instantly changes from the lowest to the highest value (a kind of negative decrease).
So the algorithm uses two functions plus their inversions to create the Yin Yang Fire.
3. Scientific Aspects
3.1 The cycles
A) Snapshot of the lowest average cell value during a cycle
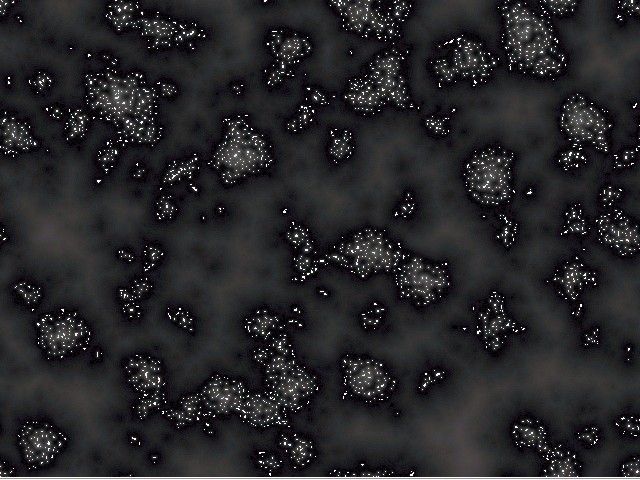
B) Snapshot of the highest average cell value during a cycle
One cycle between the minimum and the maximum average cell value needs about 490 timesteps (using 256 states).
3.2 The system-evolution
Cell-like patterns
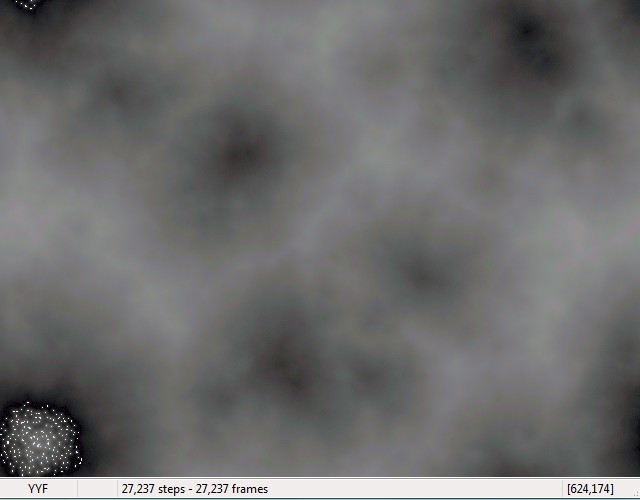
Because the ignition-areas are unsychronized and because of selforganizing effects, some areas start to dominate the ignition process after a while and start to form cell-like patterns (see left bottom of the picture above). This happens at approximately 30,000 steps (using 256 states).
Overlapping of cycles

At approximately 60,000 steps (using 256 states) the phases of ignitions of spakles and the die out of sparkles start to overlap. At that time the differences between minimum and maximum of the average cell value decreases.
And as reported by Ruijs, the cell-like structures are only an intermediate result. As the phases overlap more and more, the patterns start to get more fractalized again.
3.3 The Excel-Modell
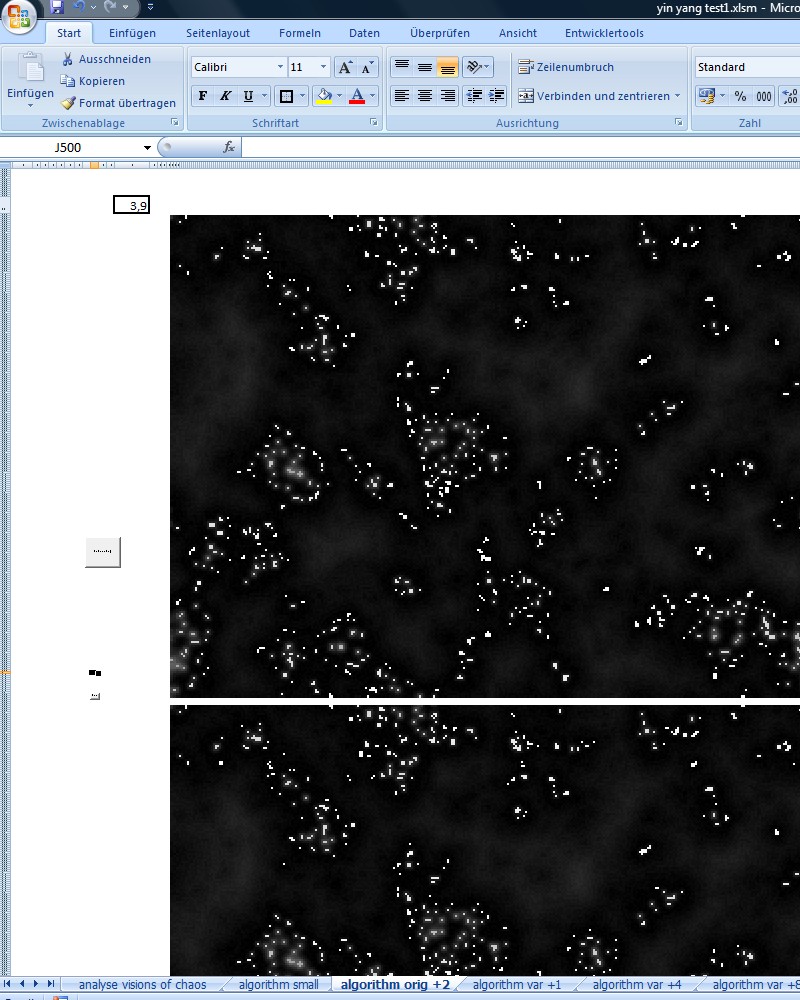
To study the behaviour of the algorithm in detail, I build an Excel-Modell (Excel 2007) using Conditional Format, VBA coding and the function of copy and paste to emulate the memory.
In the upper left corner you can see the average cell value of the calculated matrix in every timestep.
3.4 First results
The length of the cycles
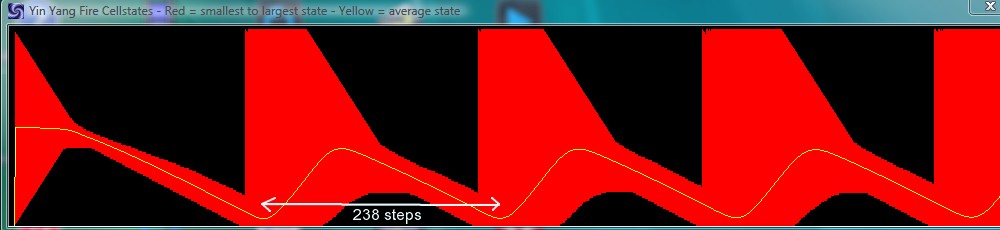
The picture above shows the mesurement of the length of a cycle that emerges with the use of 128 states.
But this lenght is not a constant value. The algorithm is very sensitive to the used number of states:
| States | 8 | 16 | 32 | 64 | 128 | 256 | 512 | |
| Cycle-length | 8 steps | 19 steps | 44 steps | 106 steps | 238 steps | 490 steps | 1000 steps | |
| Cycle-lenght / States | 1 | 1,19 | 1,38 | 1,66 | 1,86 | 1,91 | 1,95 | |
| significant overlapping of states after | 6 steps | 20 steps | 60 steps | 600 steps | 6,500 steps | 60,000 steps | ||
| cycle amplitude almost zero after | 20 steps | 120 steps | 650 steps | 5,000 steps | 40,000 steps |
The decrease of the amplitude of the cycles
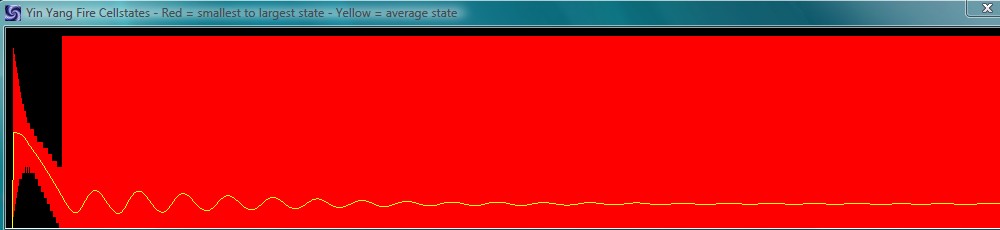
As shown in the pictue above for 32 states, the amplitude of the cycles decreases during the evolution of the system. At the end you only have very little fluctuations and the amplitude is almost zero.
The Plus value
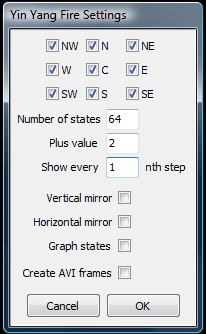
The Plus value allows you to change the parameter that is added to the average cell value in the algorithm for every step. This changes the sensitivity of the centre cell to the surrounding cells. The smaller the value the more sensitive the cell gets.
A high value on the other hand also changes the cycle lenght and makes it shorter with a different shape. In addition the behaviour of the patterns changes. You can see this in the comparison of the two pictures below, where the first 1000 cycles are shown (64 states) with a value of "+2" and then with a value of "+8":
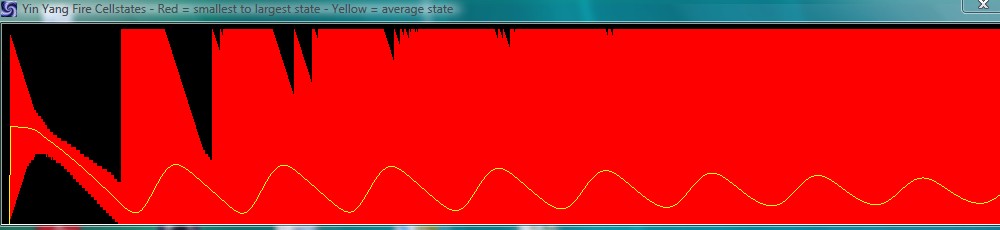
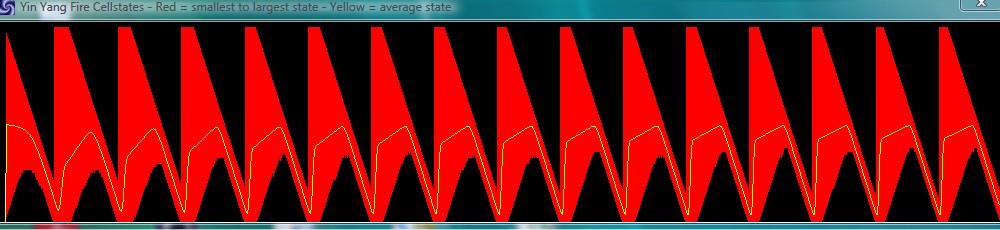
4. Things to try
Catastrophic events
For example let's now try using 255 states instead of 256 states. Surprisingly this is what you get:
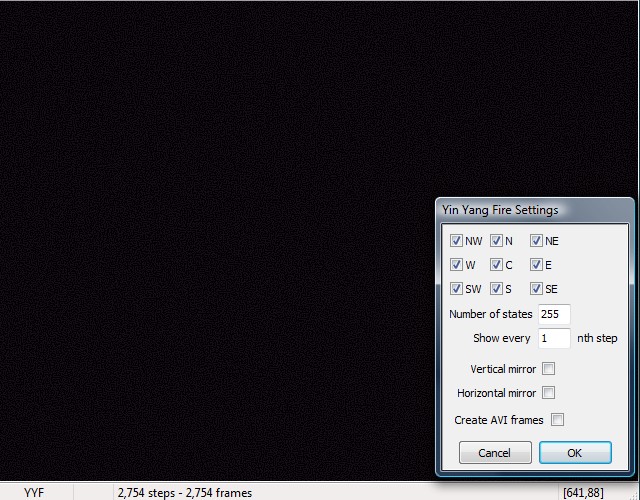
Uuups ... a catastrophic collaps of patterns after only 2500 steps!
Asymmetric neighborhoods
You can also try asymmetric neighborhoods for interesting phase-transitions. The lower the number of states, the faster the emerging transitions are.
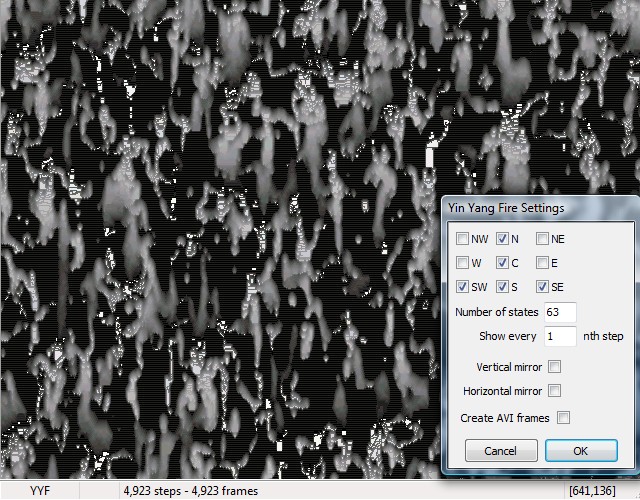
This configuration above results in strange patterns that seem to move upwards.
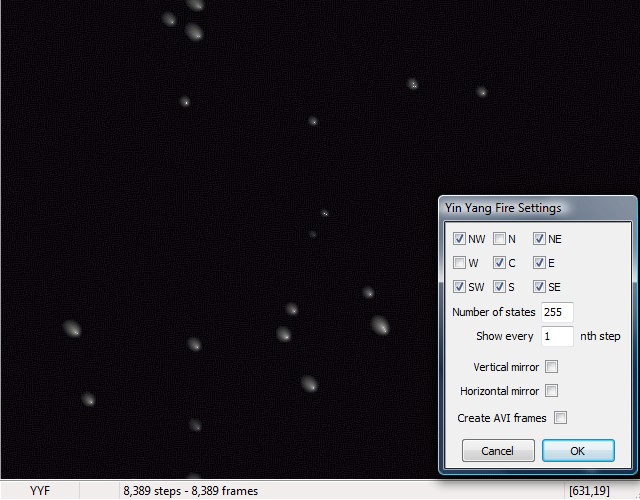
Here you get "blinking stars". The patterns almost die out ... but only almost.
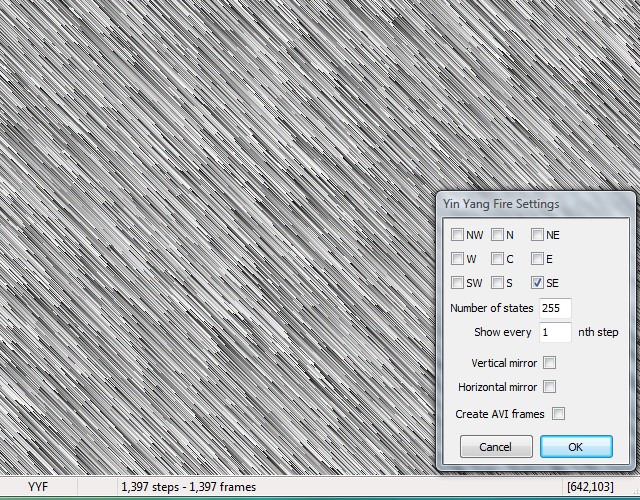
And here you get a kind of glass fiber patterns moving down.
Changing the Plus value
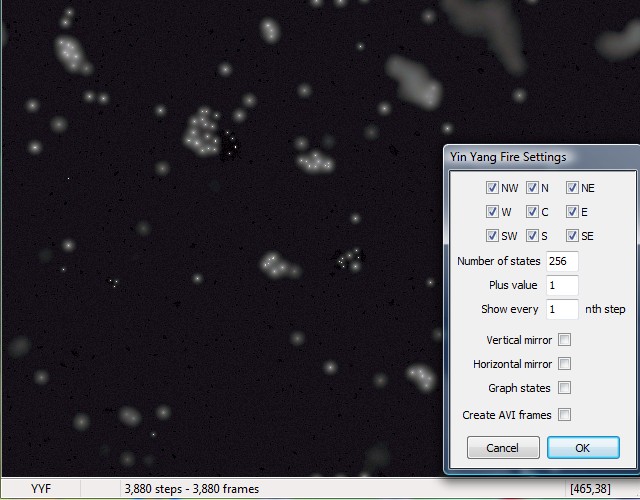
Using the Plus value 1 you can get a kind of "star nebula", where new stars are born and die out after a while.
References
Samuryo; Fire Algorithm Comparison, youtube; 2010
Jack Ruijs; Yin Yang Fire; 1999
Jason Rampe; Softology; 2015