Die Welt der Strukturwissenschaften

Strukturen der Informatik

 

Inhalt

Vorwort: Informatik als Strukturwissenschaft im Rahmen der Theoretischen Informatik

 

1. Formalen Sprachen: formale Grammatiken (=Generator) und formale Automaten (=Akzeptor)

1.1 Formale Grammatiken und Datenstrukturen

1.1.1 Rekursiv aufzählbare Sprachen, kontextsensitive und kontextfreie Sprachen

1.1.2 Reguläre Sprachen und Kontrollstrukturen

1.2 Automatentheorie und endliche Automaten

1.2.1 Formale Automaten: Turingmaschine, linear beschränkter Automat, Kellerautomat

1.2.2 Endliche Automaten

2. Berechenbarkeitstheorie

3. Komplexitätstheorie der Informatik

3.1 Berechenbarkeitskomplexität I: Rechenzeit (P und NP-Probleme)

3.2 Berechenbarkeitskomplexität II: Programmgröße (Algorithmische Komplexität)

4. Algorithmen und Computer

4.1 Deterministische Algorithmen

4.2 Randomisierte (zufällige) Algorithmen

4.3 Deterministische und Nichtlineare Optimierung

5. Modelle für komplexe Netzwerke und Systeme

5.1 Zellulare Automaten

5.2 NK-Netzwerke

5.3 Fraktale Computergrafik

6. Komplexe Evolutionäre Algorithmen als flexible Suchfunktion für Problemlösungen

6.1 Arten von Evolutionäre Algorithmen

6.2 Artificial Life - künstliches Leben

6.3 Artificial Intelligence - künstliche Intelligenz

 

 

 

 

Vorwort: Informatik als Strukturwissenschaft

Die Informatik ist zunächst ein Wissenschaftsgebiet, welches viele verschiedene Aspekte umfasst. Beispielsweise als praktische Informatik, die sich Programmierung von Software beschäftigt, oder als technische Informatik, die sich mit dem Computerbau beschäftigt, und als solche einen starken ingenieurswissenschaftlichen Charakter hat. Die Bezeichnung als genuine Strukturwissenschaft im engeren Sinne trifft daher vor allem auf den Zweig der Informatik zu, der Theoretische Informatik genannt wird. Der Informatiker Edsger Wybe Dijkstra soll dazu einmal gesagt haben: „In der Informatik geht es genau so wenig um Computer wie in der Astronomie um Teleskope.“ 

Die Theoretische Informatik beschäftigt sich daher statt mit Computern vielmehr mit der Abstraktion, Modellbildung und grundlegenden Fragestellungen, die mit der Struktur, Verarbeitung, Übertragung und Wiedergabe von Informationen in Zusammenhang stehen (siehe hier online).

Die zentralen Gedankengebäude sind - ganz ähnlich wie in der Mathematik - die Logiken als Sprache über Strukturen und die abstrakten Strukturen der Informatik selbst. Sind es in der Mathematik dabei jedoch Strukturen, wie die Gruppen oder Vektorräume, so stehen in der Informatik vielmehr Strukturen wie beispielsweise die Transitionssysteme, endliche Automaten, relationale Datenbanken, Datenstrukturen, Softwarestrukturen (Kontrollstrukturen) oder Schaltkreise im Vordergrund.

 

 

 

 

1. Formale Sprachen: formale Grammatiken und formale Automaten

 

 

1.1 Formale Grammatiken und Datenstrukturen

 

1.1.1 Rekursiv aufzählbare Sprachen, kontextsensitive und kontextfreie Sprachen

 

1.1.2 Reguläre Sprachen und Kontrollstrukturen

Die Strukturierte Programmierung ist ein programmiersprachenübergreifendes Programmierparadigma und ist heute in allen Bereichen, in denen professionelle Software entwickelt wird, eine Selbstverständlichkeit.

Auf der untersten Ebene verlangt dies die Beschränkung auf drei Kontrollstrukturen:

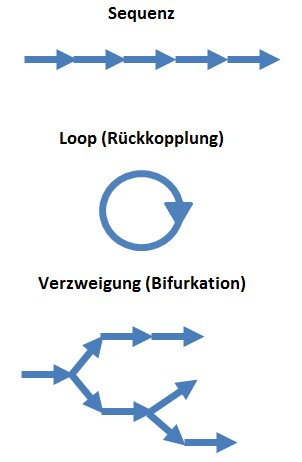
kontrollstrukturen
Bildlizenz-Info: Bild selbst erstellt, Public Domain 

 

 

1.2 Automatentheorie und endliche Automaten

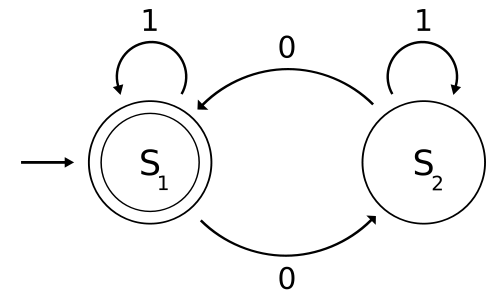
endlicher automat
Bildlizenz-Info: Endlicher Automat, Wikipedia, Public Domain

 

1.2.1 Formale Automaten: Turingmaschine, linear beschränkter Automat, Kellerautomat

 

1.2.2 Endliche Automaten

Ein endlicher Automat (EA, auch Zustandsmaschine oder Zustandsautomat; englisch: FSM, finite state machine) ist ein Modell eines Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen.

Ein Automat besteht aus:

Eine Transitionsrelation (auch Übergangsrelation) ist in der Informatik eine Relation, die mögliche Übergänge beschreibt.

In Transitionssystemen und bei Automaten gibt eine Transitionsrelation an, welche Zustandswechsel möglich sind. Man spricht dann auch von einer Zustandsübergangsrelation. Eine Transitionsrelation ist aber nicht auf Zustandswechsel beschränkt. Befinden sich zwei Zustände in Relation, so ist ein direkter Wechsel von einem Zustand in den anderen möglich, andernfalls nicht. Es ist auch möglich, dass die Relation aus weiteren Parametern besteht, etwa einem Eingabesymbol, von dem der Zustandswechsel abhängt. Für Zustandsübergänge nach beliebig langen Eingaben verwendet man die reflexive und transitive Hülle einer Transitionsrelation.

Transitionen werden auch durch Funktionen definiert. Man spricht dann von Transitionsfunktionen oder Übergangsfunktionen.

Akzeptoren

Akzeptierende Automaten sind ein einfaches Modell, jedoch ist der Formalismus für viele Anwendungen zu eingeschränkt.

Transduktoren (Transducer)

Endliche Automaten, die zusätzlich zum lesen auch noch schreiben können, werden Transducer genannt.

Rekursive Transitionsnetzwerke (RTN)

Die RTN, die auch rekursive Übergangsnetze genannt werden, kann man durch Automaten oder durch Petrinetze beschreiben. Die Anwendungsgebiete dieser mathematischen Modelle sind meist Systeme, die kontinuierlich auf ihre Umwelt reagieren müssen. Durch die exakte Spezifikation sind beweisbare Aussagen über diese Systeme möglich.

Ein Transitionsnetz ist ein gerichteter Graph. Je nach Typ haben Kanten und Knoten unterschiedliche Bedeutungen. Bei Automaten entsprechen die Knoten den Zuständen des Systems und die Kanten den Ereignissen, die zu Zustandsübergängen führen.

 

 

 

 

2. Berechenbarkeitstheorie

Die Berechenbarkeitstheorie der Theoretischen Informatik fragt danach, wie eine Berechenbarkeit überhaupt mathematisch formalisiert werden kann.

Weiterhin wird gefragt, welche Aufgaben eine Maschine unabhängig von der physischen Realisierbarkeit prinzipiell überhaupt lösen kann.

Entscheidbarkeit und unentscheidbare Probleme

Ein Problem heißt entscheidbar, wenn es durch einen Algorithmus gelöst, bzw. entschieden werden kann. Es gibt in der Informatik vielerlei entscheidbare Problemklassen, jedoch sind auch einige Probleme prinzipiell unentscheidbar.

So sind beispielsweise nach dem Satz von Rice alle nichttrivialen semantischen Eigenschaften von Programmen unentscheidbar. Weiterhin kann das Problem der Gültigkeit prädikatenlogischer Aussagen nicht algorithmisch gelöst werden. Die Aufgabe, eine Aussage der Prädikatenlogik daraufhin zu überprüfen, ob sie wahr oder falsch ist, ist laut Church und Turing ein unlösbares Entscheidungsproblem. Das Gleiche gilt auch für das sogenannte Halteproblem der Informatik, d.h. wann und ob ein gegebenes Programm jemals an ein Ende gelangen wird, ist unentscheidbar.

Die Berechenbarkeitstheorie führt uns daher in den Bereich der Entscheidbarkeit von Problemen. Es gibt dabei drei Arten von Problemen: entscheidbare Probleme, semientscheidbare Probleme (die je nach Bezug mal entscheidbar und mal unentscheidbar sind) und unentscheidbare Probleme. Diese Arten greift die Komplexitätstheorie der Informatik auf, und bildet speziell für die entscheidbaren Probleme dann verschiedene Komplexitätsklassen aus.  

 

 

 

 

3. Komplexitätstheorie der Informatik

Entscheidbare Probleme (siehe SAT-Problem; "Satisfiability") müssen nicht immer auch "einfach" sein. Eine Art, die Komplexität für entscheidbare Probleme in Klassen zu definieren erhält man, wenn man die dazu benötigte Rechenzeit betrachtet.

 

3.1 Berechenbarkeitskomplexität I: Rechenzeit (P und NP-Probleme)

p_np
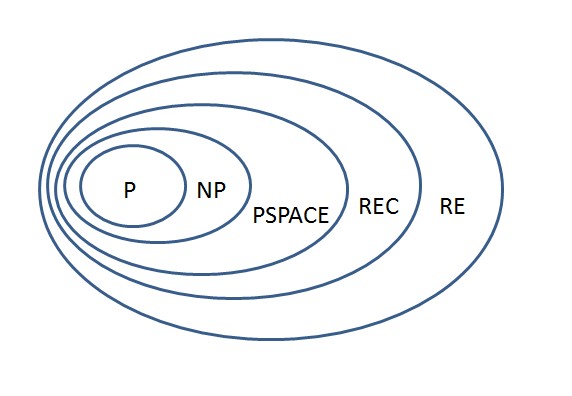
Bildlizenz-Info: Bild selbst erstellt, Public Domain

Hierbei wird die Rechenzeit von Algorithmen in Abhängigkeit der Länge ihres Inputs bestimmt. Probleme, die in polynomialer Zeit mit einer deterministischen Turingmaschine gelöst werden können, heißen "P"-Probleme.

Probleme, die in polynomialer Zeit von nichtdeterministischen Turingmaschinen (zufallsgesteuerte Automaten) gelöst werden können, heißen "NP"-Probleme.

Die nächsthöhere Komplexitätsklasse bilden die sogenannten "PSPACE"-Probleme, bei denen die Lösungen exponentiell lang sein können. Die Lösungssuche kann hier sehr lange dauern.

Alle überhaupt algorithmisch lösbaren Probleme bilden die Klasse "REC" (recusively decidable).

In der obersten Klasse sind für die Lösungskandidaten keine oberen Schranken angebbar. Diese Probleme sind "RE" (recursively enumerable), da algorithmisch unendlich viele Lösungen ausgegeben werden können.

 

3.2 Berechenbarkeitskomplexität II:  Programmgröße (Algorithmische Komplexität)

Von Chaitin und Komolgorov stammt der Vorschlag, die algorithmische Komplexität einer Symbolfolge s durch die Länge des kürzesten Computerprogramms zur Erzeugung von s (gemessen in Bit) zu definieren. Diese algorithmische Komplexität wird auch als algorithmischer Informationsgehalt einer Symbolfolge bezeichnet.

Eine einfache Abfolge von Bits mit vielen Regelmäßigkeiten und Wiederholungen kann daher mit einem kurzen Computerprogramm bewerkstelligt werden. Bei einer Zufallsfolge gibt es jedoch keinen kürzeren Algorithmus, als die Zufallsfolge selbst. Das "Programm" entspräche demnach genau der Zufallsfolge, und wäre ohne Beschränkungen unendlich lang.

Ein Kritikpunkt dieser Art der Komplexitätstheorie ist daher, dass danach ausgerechnet Zufallsfolgen die höchste Komplexität besitzen sollen.

 

 

 

 

4. Algorithmen und Computer

 

4.1 Deterministische Algorithmen

 

4.2 Randomisierte Algorithmen

 

4.3 Deterministische und Nichtlineare Optimierung

Deterministische Verfahren heißen deterministisch, weil sie immer ein identisches Verhalten zeigen, wenn man sie am gleichen Startpunkt beginnen lässt. Die Art, die Suchrichtung zu bestimmen, teilt diese Verfahren in zwei große Gruppen ein. Man spricht von indirekten Verfahren, wenn dazu Informationen der partiellen Ableitung der Qualitätsfunktion benötigt werden und von direkten, wenn stattdessen Qualitätsfunktionswerte unter Anwendung von Heuristiken genügen.

Ausgehend vom Vektor des Startpunkts bzw. des zuletzt ermittelten Punkts werden Suchrichtung und Schrittlänge ermittelt, um daraus einen neuen Punkt zu berechnen. Dieser wird dann bewertet und das Abbruchkriterium überprüft. Die Verfahren unterscheiden sich vor allem in der Ermittlung der Suchrichtung und der Schrittlänge.

Im Unterschied zu den deterministischen Optimierungen gibt es auch die flexibleren evolutionären Algorithmen zur Problemlösung.

 

 

 

5. Modelle für komplexe Netzwerke und Systeme

 

5.1 Endliche Automaten: Zellulare Automaten1

 

5.1.1 Eindimensionale zellulare Automaten

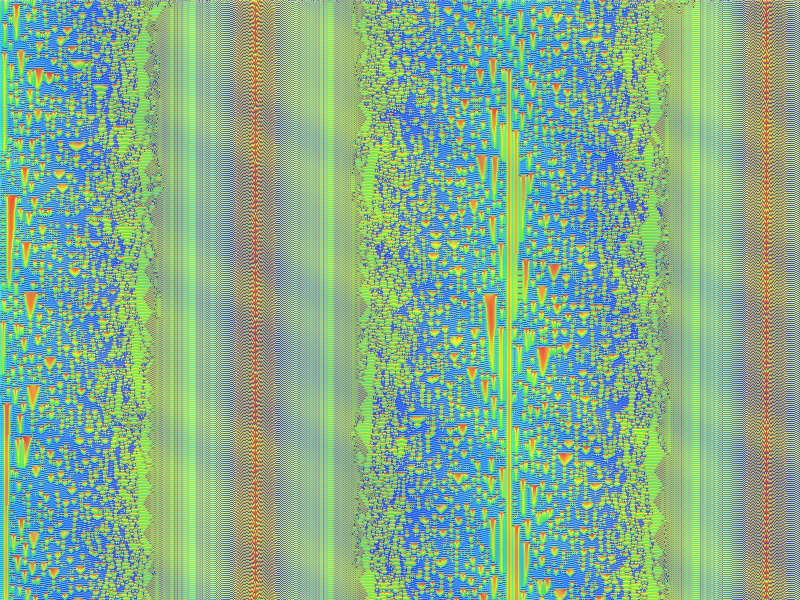
testing
Bildlizenz-Info: Bild selbst erstellt mit dem Freeware-Programm Gimp2, Render-Muster: "CML-Explorer"; Public Domain

Ein zellularer Automat ist ein diskretes dynamisches System, das sich durch wiederholte Anwendung einfacher deterministischer Regeln entwickelt und stellt ein Beispiel für einen endlichen oder unendlichen Automaten dar. Genau genommen handelt es sich hierbei um einen Spezialfall eines Automatennetzwerkes. Ein weiterer Fachausdruck dafür ist das sogenannte "Gekoppelte Abbildungsgitter (engl. "Coupled-Map Lattice").

Aus Sicht der theoretischen Informatik handelt es sich hierbei zusätzlich um einen Parallelrechner. Bereits 1971 konnte Alvin Ray Smith beweisen, dass jede Turing-Maschine durch einen zellularen eindimensionalen Automaten simuliert werden kann, der somit zu Lösung von hochkomplexen Aufgaben fähig ist2.

Einen zellularen Automaten kann man als eigenes logisches Universum mit einer eigenen "Physik" betrachten. Und so ein ZA-Universum kann trotz seiner einfachen Konstruktion komplexes und überraschendes Verhalten zeigen, welches sich sowohl für das anhaltende technische, also auch das philosophische Interesse der Informatiker verantwortlich zeichnet.

Eindimensionale zellulare Automaten als Modelle für dynamische Systeme

Das dynamische Verhalten zellularer Automaten kann allgemein als komplex bezeichnet werden. Stephen Wolfram schlug aufgrund umfangreicher Simulationen folgende Einteilung eindimensionaler zellularer Automaten in vier Klassen vor:

  1. Jeder Anfangszustand konvergiert zu einem Fixpunkt.
  2. Jeder Anfangszustand endet in einer Schleife von sich wiederholenden Zuständen.
  3. Es treten fraktale Muster und beliebige Perioden auf.
  4. Es treten symmetriebrechende Konfigurationen und langlebige lokale Muster auf.

In der Tradition der Chaostheorie spricht man bei periodischen Schleifen, auf die sich die Anfangszustände hinentwickeln, von Attraktoren. Zellulare Automaten können auch in dem Sinn chaotisches Verhalten aufweisen, als dass minimale Veränderungen in der Ausgangskonfiguration in enormen Unterschieden in späteren Generationen resultieren können.

 

5.1.2 Zweidimensionale zellulare Automaten und Conways "Spiel des Lebens" (Conway's Game of Live)

GOL
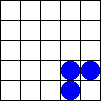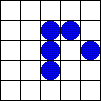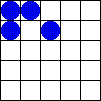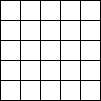
Bildlizenz-Info: GameOfLife_Glider_Animation; Wikipedia; Public Domain

In einem eindimensionalen zellularen Automaten werden lediglich einzelne (eindimensionale) Zeilen miteinander logisch gekoppelt, und erzeugen dabei einen Output nach einer bestimmten Regel.

Bei zweidimensionalen zellularen Automaten dient als Basis für den nächsten Rechenschritt die komplette (zweidimensionale) Nachbarschaft einer Fläche. In Abhängigkeit von der Population einer definierten Nachbarschaft werden dann Zellen entweder gefüllt, oder gelöscht.

Die dabei entstehenden, komplexen Gebilde, die sich über dem Bildschirm bewegen und auftauchen und wieder verschwinden erinnern entfernt an eine gewisse "Lebendigkeit" des Bildschirms. Auf dem Spielfeld zeigt sich mit jedem Generationsschritt eine Vielfalt komplexer Strukturen. Einige typische Objekte lassen sich aufgrund eventuell vorhandener besonderer Eigenschaften in Klassen einteilen: sie verschwinden, bleiben unverändert, verändern sich periodisch (oszillieren), bewegen sich auf dem Spielfeld fort, oder wachsen unaufhörlich.

 

 

5.2 NK-Netzwerke

 

5.3 Fraktale Computergrafik

Einfache, selbstähnliche Abbildungen durch IFS:

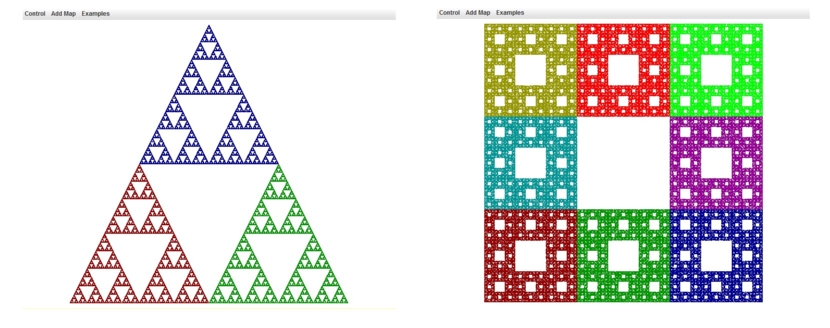
sierpinski und teppich
Bildlizenz-Info: Freeware-Programm Chaos Game (IFS.jar), Public Domain; von David Eck; online

Eine einfache IFS-Animation:

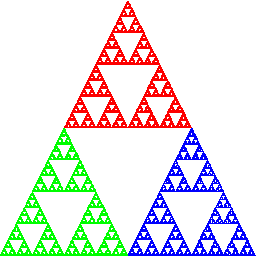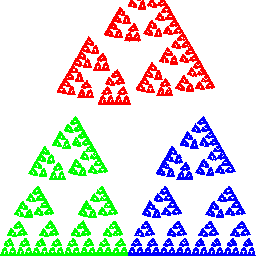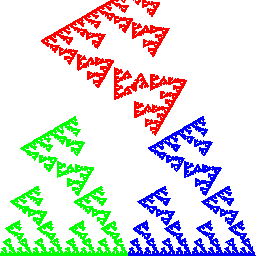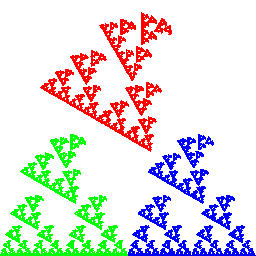
ifs-ani2
Bildlizenz-Info: Chaos Game, gif-Animation mehrerer Einzelbilder, Public Domain

 

 

 

 

6. Evolutionäre Algorithmen als flexible Problemlösungsalgorithmen

 

6.1 Arten von Evolutionären Algorithmen

Zur Gruppe der Evolutionären Algorithmen gehören:

Evolutionäre Strategien

Evolutionäre Strategien basieren zunächst hauptsächlich auf der Beobachtung, dass die Kinder den Eltern ähnlich sind und dass eine Art "Evolutionsfenster" existiert. Ist nämlich die Variation der Kinder zu gering, so ergibt sich nahezu keine Evolution, ist sie hingegen zu groß, so sind die Nachkommen mehrheitlich viel schlechter als die Eltern. Diese Beobachtung wird durch die Angabe einer Wahrscheinlichkeitsverteilung präzisiert und entsprechend implementiert. Dies erinnert stark an die Wahrscheinlichkeitsverteilung bei Simulated Annealing (simulierter Abkühlungsvorgang). Tatsächlich wurde bei ES zuerst mit einer Population von zwei Individuen (1 Elter, 1 Kind) und einem einfachen Mutation-Selektions-Mechanismus (ohne geschlechtliche Fortpflanzung) gearbeitet. Dabei wurde bei der Selektion im Prinzip entschieden, ob Elter oder Kind überleben soll.

Genetische Algorithmen

Genetische Algorithmen nehmen zunächst die biologische Unterscheidung Genotyp/Phänotyp ernst. Dabei repräsentiert üblicherweise ein Bitstring den Genotyp eines Individuums. Im Bitstring können verschiedenartigste Objekte codiert sein. Diese Codierung entspricht dem Übergang von Genotyp zum Phänotyp. Bei der Parameteroptimierung kann ein Ort im Parameterraum auf unterschiedlichste Art und Weise in einen Bitstring codiert werden.

Ablaufschema bei einem Genetischen Algorithmus:

Die Evolution ist in der Lage, durch Manipulation des Erbgutes selbst komplexe Lebensformen und Organismen an ihre Umwelt- und Lebensbedingungen anzupassen. Sie löst damit ein sehr schwieriges Optimierungsproblem. Die erstaunlichste Eigenschaft der Evolution ist die relative Einfachheit ihrer Vorgehensweise und das Zusammenwirken der verschiedenen Steuerungsmechanismen. In einem einfachen Modell der genetischen Algorithmen lässt sich der durchgeführte Suchprozess auf drei biologische Prinzipien zurückführen: Mutation, Rekombination und Selektion.

Die Mutation des Erbgutes ist ein ungerichteter Prozess, dessen Sinn einzig in der Erzeugung von Alternativen und Varianten liegt. Aus Sicht der Optimierungstheorie kommt der Mutation die Aufgabe zu, lokale Optima zu überwinden. Genetisch entspricht dies neuem Erbgut, das in die Population eingeführt wird und deren Diversität erhält.

Die Rekombination (Crossover) der Erbinformation liegt hinsichtlich ihres Beitrages zur Zielfindung im Rahmen der Evolution zwischen Mutation und Selektion. Die Stellen, an denen ein Crossover zwischen homologen Chromosomen stattfindet, werden zufällig bestimmt. Die eigentliche Rekombination erfolgt aber nicht mehr zufällig. Nahe beieinanderliegende und funktional verbundene Gene werden seltener getrennt als weiter auseinanderliegende Gengruppen. Ein evolutionärer Algorithmus kann ohne Rekombination auskommen (d.h. es gibt eine asexuelle Fortpflanzung der einzelnen Individuen mit nur einem Elternteil pro Kind), in bestimmten Fällen ist die Anwendung von Rekombination jedoch effizienter.

Die Selektion ist für die eigentliche Steuerung der Suchrichtung der Evolution zuständig. Sie bestimmt die Richtung, in der sich das Erbgut verändert, indem sie festlegt, welche Phänotypen sich stärker vermehren. Die Selektion wäre demnach, wenn es keine Störungen gäbe, eine deterministische Komponente innerhalb der Evolution. In der Natur wird die Selektion jedoch immer wieder durch meist zufällige Ereignisse gestört. Auch die am besten an ihre Umgebung angepassten Individuen können durch ein Unglück sterben, bevor sie Nachkommen zeugen. Damit würde die genetische Information, die ein Optimum darstellt, verloren gehen. Zwei weitere Einflüsse machen die Selektion zu einem indeterministischen Faktor. Zum einen ist sie keine konstante Größe, da sich die Umwelt und die Lebensbedingungen der Individuen ändern können, zum anderen gibt es eine Rückkopplung zwischen den einzelnen Individuen und ihrer Umgebung. Diese können durch Eingriffe in die Umwelt ihre eigene Selektion beeinflussen.

Algorithmisch kommt der Repräsentation der Individuen große Bedeutung zu. Wie wird eine potentielle Lösung genetisch kodiert? Was ist der Lösungsraum? Welche Variationsoperationen sind darin angebracht? Dies muss meist problemabhängig beantwortet werden, typische Repräsentationen sind Datenstrukturen wie Vektoren von Bits, reellen Parametern oder ganze Programme.

Daneben ist die Bewertungsmethode, auch Fitnessfunktion genannt, essentiell für die Leistung des genetischen Algorithmus. Sie muss in der Lage sein, die Qualität beliebiger Lösungen möglichst gut abzubilden, da sie das Selektionskriterium bildet und damit die Suchrichtung definiert. Grundregeln sind, dass die optimale Lösung maximal bewertet werden sollte, während ähnliche Lösungen ähnlich bewertet werden sollten. Außerdem helfen möglichst feine Abstufungen zwischen "schlechten" und "guten" Lösungen dem Suchvorgang. Typischerweise ist die Bewertung der rechenintensivste Teil eines genetischen Algorithmus. In der Regel werden einzelne Individuen unabhängig bewertet, indem sie auf einen reellen Wert abgebildet werden. Allerdings sind auch "Tournament"-Verfahren üblich, die jeweils eine Teilgruppe von Individuen betrachten und diese relativ vergleichen und Werte zuweisen. Je strenger das Bewertungsverfahren und die damit verbundene Selektion arbeiten, desto höher ist der Selektionsdruck. Je höher der Selektionsdruck, desto schneller konvergiert die Population gegen ein Optimum, desto höher ist jedoch auch die Gefahr, dass dies nur ein lokales Optimum ist.

Memetische Algorithmen

Darunter versteht man Optimierung des genetischen Codes durch Überleben der besten Individuen und ist eine Kombination aus der globalen Suche durch eine ganze Population und der lokale Suche durch jedes einzelne Individuum.

Ablaufschema:

Beim Wettkampf greifen Individuen einander an oder werden angegriffen. Die Verlierer werden aus der Liste entfernt. Bei der Kooperation werden Komponenten von Individuen ausgetauscht um ein neues Individuum zu erschaffen (entspricht beim Genetischen Algorithmus dem Crossover).

 

6.2 Artificial Life - künstliches Leben

 

 

6.3 Artificial Intelligence - künstliche Intelligenz

 

 

 

 

 

Einzelnachweise

1 Elisabeth Rembold; Zellulare Automaten; 1996 online

2 Smith, A. R., Simple Computation-Universal Cellular Spaces, J. ACM, 1971