Die Welt der Strukturwissenschaften

Komplexe Strukturen der Systemwissenschaften

 

Inhalt

Vorwort: Klassiker der Systemwissenschaft - die Allgemeine Systemtheorie und die Kybernetik

 

1. Strukturelle Grundlagen Dynamischer Systeme

1.1 Dynamische Systeme und axiomatische Formalisierung

1.2 Analyse Dynamischer Systeme

1.3 Unterschiedliche Eigenschaften linearer und nichtlinearer Systeme

1.4 Konservative Systeme

1.5 Dissipative Systeme

1.6 Ausblick: Die spannende strukturwissenschaftliche Erforschung nichtlinearer Systeme

 

2. Die Systemdynamik elementarer Dynamischer Systeme

2.1 Systemdynamik 0: Statische, speicherlose Systeme

2.2 Systemdynamik I: Systeme mit einer Zustandsgröße

2.3 Systemdynamik II: Schwingungsfähige Systeme

2.4 Systemdynamik III: Chaostheorie und deterministisches Chaos

2.4.1 Bedingungen für chaosfähige Systeme

2.4.2 Beispiele einfacher chaosfähiger Systeme

2.5 Systemdynamik IV: Selbstorganisation

2.6 Systemdynamik V: Zufällige Dynamik und Random Walk

2.7 Systemdynamik VI: Die Evolution von elementaren komplexen Systemen

 

3. Räumlich ausgedehnte Systeme: Struktur- und Musterbildung in komplexen Netzwerken

3.1 Wichtige Eigenschaften komplexer dynamischer Netzwerke

3.1.1 Autopoiese

3.1.2 Selbstorganisation

3.1.3 Synergetik

3.1.4 Dissipative Strukturen

3.1.5 Chaotic itinerancy (chaotische Wanderschaft) - zwischen Selbstorganisation und Chaos

3.2 Kohärente Strukturen: Nichtlineare Wellen, Solitonen

3.2.1 Wandernde Wellen (Burgers, Korteweg, de Vries), Schockwellen

3.2.2 Mehrsolitonen-Lösung

3.3 Musterbildung in Reaktions-Diffusions-Systemen

3.3.1 Turing-Strukturen

3.3.2 Aktivator-Inhibitor-Modelle

3.3.3 Brüsselator

3.3.4 Oregonator

3.3.5 Die Komplexe Ginzburg-Landau-Gleichung

3.4 Kauffman-Netzwerke

3.5 Gekoppelte Abbildungsgitter (CML)

3.5.1 Elementare CMLs

3.5.2 CNNs

3.5.3 Zellularautomaten

3.6 Zellularautomaten

3.6.1 Elementare und totalistische Zellularautomaten

3.6.2 Game of life und Varianten

3.7 Zufallsdynamik räumlich ausgedehnter Systeme

3.8 Die Evolution komplexer Netzwerke

 

 

 

 

Vorwort: Klassiker der Systemwissenschaft - die Allgemeine Systemtheorie und die Kybernetik

 

Allgemeine Systemtheorie

Um etwa 1950 führte Ludwig von Bertalanffy die allgemeine Systemtheorie als ein neues wissenschaftliches Paradigma ein, das er als Gegenentwurf zur klassischen Physik positionierte. Er kritisierte deren deduktive Verfahren und die damit einhergehende isolierte Betrachtung von Einzelphänomenen. Für die Biologie sei diese Methode nicht adäquat. Anstelle von Einzelphänomenen, die in der Realität niemals isoliert aufträten, seien diese Phänomene in ihrer Vernetzung zu beschreiben.

Daher setzte er der isolierten Einzelbetrachtung den Systembegriff entgegen, wobei dieser Begriff eine Menge von Elementen und deren Relation untereinander beschreiben soll. Als ein solches Modell betrachtete er die „organisierte Komplexität“. Während die klassische Wissenschaft „unorganisierte Komplexität“ erfolgreich beschrieben habe, stehe die theoretische Erfassung organisierter Komplexität vor neuen Herausforderungen. Organisierte Komplexität sei gegeben, wenn Einzelphänomene nicht schlicht linear logisch miteinander gekoppelt seien, sondern Wechselwirkungen unter ihnen bestünden. Sei dies der Fall, könne eine exakte Beschreibung der reziproken Vernetzungsbedingungen ein Bild von der Einheit der Summe jener Einzelphänomene vermitteln.

Die Systemlehre untersucht somit die Organisationsformen komplexer Wechselbeziehungen zwischen einzelnen Elementen jenseits linear darstellbarer Relationen und einfacher Kausalität. Dabei unterschied von Bertalanffy zwischen offenen und geschlossenen Systemen. Ein geschlossenes System wird als binnenstabil und über keine Wechselwirkungen mit der Umwelt verfügend beschrieben. In einem solchen System gibt es strenggenommen keine organisierte Komplexität, da sich die Elemente im Gleichgewichtszustand in mathematisch eindeutiger Weise zueinander verhalten. Ein offenes System dagegen verfügt über variabilisierte Relationen seiner Elemente, die durch nichtprognostizierbare Umwelteinflüsse verändert werden.

Die interne Variabilität ermöglicht es dem System, sich in einem dynamischen Umfeld relativ zu stabilisieren (Fließgleichgewicht). Offene Systeme entfalten also im Austausch mit ihrer Umwelt eine Dynamik und variieren ihre Zuständlichkeit, ohne dabei ihre Systemstrukturen vollständig ändern zu müssen. Sie zeichnen sich dadurch aus, dass sie nicht kausal von außen beeinflusst werden, sondern ihre interne Organisation bei Umweltveränderungen selbst umstellen („Black Box“-Theorem). Dies wird als Selbstorganisation bezeichnet und kann als Paradigma organisierter Komplexität gelten.

Kybernetik

Ebenfalls um etwa 1950 schuf Norbert Wiener die Wissenschaft über die "Kunst des Steuerns" - die Kybernetik - als Lehre der Steuerung und Regelung von Maschinen und lebenden Organismen. Die Kybernetik erforscht die wesentlichen Eigenschaften von dynamischen Systemen, damit diese die relevanten Informationen verarbeiten können und die Systeme zielgerecht gelenkt werden bzw. sich selbst entsprechend lenken.

Für die Bildung kybernetischer Modelle werden die Struktur und das Verhalten der dynamischen Systeme erforscht. Die Struktur eines dynamischen Systems ist durch die Systemgrenzen, die Teilsysteme und die Elemente der Teilsysteme gekennzeichnet. Die Beziehungen zwischen den Strukturelementen, d.h. zwischen dem System und seiner Umwelt, zwischen den Teilsystemen und zwischen allen einzelnen Systemelementen, werden durch den Fluss von Materie, Energie und/oder Informationen hergestellt. Sie werden im kybernetischen Modell in Relationen überführt. Das Verhalten eines Systems wird durch die Art dieser Beziehungen bzw. Relationen charakterisiert.

Hierbei interessieren u.a. folgende Fragen: Ist das System stabil? D.h., strebt es einem Gleichgewichtszustand (trotz Störungen) zu? Bei welcher Größenordnung einer Störung ist das weitere Bestehen des Systems gefährdet? Welche Zeit benötigt ein System, um eine Störung zu bewältigen? Treten bleibende Regelabweichungen auf, d.h., bleibt das System auch nach langer Zeit noch vom Gleichgewichtszustand entfernt? Ist das System beobachtbar und steuerbar?

 

 

 

 

1. Strukturelle Grundlagen von Systemen

 

 

1.1 Dynamische Systeme und axiomatische Formalisierung¹

Komplexe dynamische Systeme in Technik, Umwelt, Wirtschaft und Gesellschaft bestimmen mit ihrem oft überraschenden Verhalten die Entwicklung unserer Welt. Die komplexen Wirkungsstrukturen mit ihren vielfachen und meist nichtlinearen Verknüpfungen der Systemelemente sind ohne umfassende Modellbildung kaum zu verstehen.

Darüber hinaus kann erst die Simulation mit einem gültigen Modell das ganze Spektrum der Entwicklungs- und Eingriffsmöglichkeiten darstellen. Abstrakte Modellbildung und Simulation sind daher unentbehrliche Hilfsmittel für das Verständnis unserer Welt und für den "vernünftigen" Umgang mit ihr geworden. 

 

Die Methode der "System Dynamics"

Doch wie können wir uns das notwendige Verständnis auf der Basis der in den Systemwissenschaften etablierten Zustandsraumanalyse schrittweise erarbeiten? Zunächst benötigen wir ein grundsätzliches Wissen zu Systemen und Modellen.

Dazu benötigt man zunächst Kenntnis von der Systemstruktur, welche über die Identifizierung der Systemelemente und der verhaltensbestimmenden Systemstruktur gewonnen wird.

Der Systemzustand erschließt sich über die Einführung der (Vektor-)Zustandsgleichungen mit ihren Elementen der Eingangsgrößen, der Zustandsgrößen und deren Veränderungsraten.

Für ein gegebenes System ist zum weiteren Erkenntnisgewinn dann die Untersuchung des Systemverhaltens, des Systementwurfs und der mathematischen Systemanalyse notwendig.

 

Die Grundstruktur eines Systems

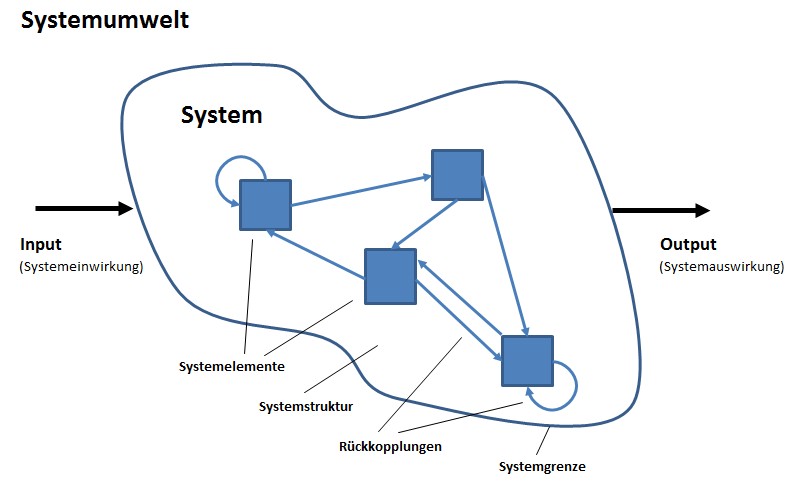
Die Basis-Systeme, die in den Systemwissenschaften und im Rahmen der Systemtheorie beschrieben werden, sind aus mathematischer Sicht bereits recht komplexe, multiple Strukturen.

Bildlizenz-Info: Bild selbst erstellt, Public Domain

Systeme bestehen zunächst aus den Systemelementen und deren Relationen, also entsprechen einer mathematischen relationalen Struktur. Die relationalen Strukturen, die als Pfeile dargestellt sind, entsprechen einer Ordnungsstruktur (inklusive der Beziehungen zum Input und dem Output).

Weiterhin besitzt jedes System eine Systemgrenze, mit der es sich von der umgebenden Umwelt abgrenzt. Dies ist eine topologische Struktur.

Und als drittes gibt es bei dynamischen Systemen Veränderungen, Transformationen und Prozesse, die mit Hilfe von algebraischen Strukturen beschrieben werden.

Neben diesen Paket aus allen verfügbaren basalen mathematischen Grundstrukturen, prägt die jeweilige speziell untersuchte Systemform und deren spezielles Systemverhalten dieser komplexen Struktur noch weitere strukturelle Merkmale auf.

Ein besonderes basales Strukturierungselement ist bei dynamischen System die Einführung und Berücksichtigung der Zeit bzw. des Zeitverhaltens eines Systems als weitere Ordnungsstruktur. Bei einem System, das sich über die Zeit nicht verändert spricht man von dem Spezialfall des statischen Systems. Doch auch Systeme, die zunächst statisch erscheinen, wie beispielsweise ein Stuhl oder ein Haus unterliegen dynamischen Belastungen und Alterserscheinungen. Es gibt kaum ein reales System, das wirklich auch über kosmologische Zeiträume hinweg unverändert bleibt.

Bei den Systemelementen unterscheidet man in den Modellen der System Dynamics ebenfalls mindesten drei Arten:

• die Vorgabegrößen, die nicht von System selbst beeinflusst werden
• die Zustandsgrößen (Speichergrößen) und ihre Veränderungsraten
• die Zwischengrößen (Wandler), die zwischen Einwirkungen und Zustandsgrößen bzw. Veränderungsraten stehen

 

Die mathematische Formalisierung der Systemzustände und des Systemverhaltens

Bei den angewandten mathematischen Methodik werden sowohl "punktförmige" einzelne Systeme, sowie auch räumlich ausgedehnte Netzwerke von Systemen modelliert. In Bezug auch die Unterscheidung von kontinuierlichen und diskretisierten Größen ergibt sich folgende Klassifizierung:

Modellierungsverfahren	Raum	Zeit	Zustand
partielle_Differentialgleichungen_(PDE)	kontinuierlich	kontinuierlich	kontinuierlich
Differentialgleichungen_(ODE)	diskret	kontinuierlich	kontinuierlich
Differenzengleichungen	diskret	diskret	kontinuierlich
Zellularautomaten	diskret	diskret	diskret

 

Lineare Gleichungssysteme

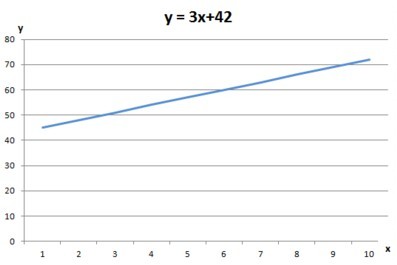
Bei linearen Gleichungssystemen liegen Gleichungen vor, bei denen die Variablen ausschließlich in der ersten Potenz vorliegen.

Ein Beispiel wäre die Gleichung y = 3x + 42. Ausführlich geschrieben lautet sie in Bezug auf die Linearität: y¹ = 3x¹ + 42. Zeichnet man dazu einen Funktionsgraf, so ergibt sich bei linearen Gleichungen immer eine gerade Linie, die verschiedene Steigungen aufweisen kann. Wenn man also einen Graphen sieht, dann kann man immer mit einem Lineal feststellen, ob ein linearer Verlauf vorliegt.

Bildlizenz-Info: Bild selbst erstellt mit Excel; Public Domain

 

Nichtlineare Gleichungssysteme

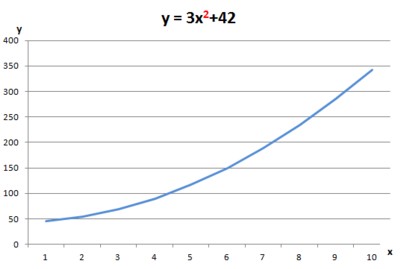
Alle Gleichungen, bei denen die Variablen nicht in der ersten Potenz vorliegen, sind nichtlineare Gleichungen.

Ein Beispiel wäre die Gleichung y = 3x² + 42, oder y = 3x³ + 42, oder auch y = 3*1/x + 42. Grafisch gesehen entstehen dabei immer irgendwelche Kurvenverläufe. Diese können also nicht mehr mit dem Lineal gezeichnet werden.

Bildlizenz-Info: Bild selbst erstellt mit Excel; Public Domain

Doch warum ist die mathematische Nichtlinearität für die Erforschung der dynamischen Systeme eigentlich so interessant? Wie wir weiter unten noch sehen werden, erweitert sich das Verhaltensrepertoire eines dynamischen Systemen im nichtlinearen Falle ganz extrem, und die Untersuchung von nichtlinearen Systemen legte den Grundstein für viele modellbildende Verfahren, welche naturähnliches Verhalten oder naturähnliche Strukturen zeigen.

 

Nichtgekoppelte und gekoppelte Gleichungssysteme

Wenn wir statt nur eine Größe zu betrachten, mehrere verwenden, erhalten wir multidimensionale Gleichungssysteme. Wollen wir beispielsweise ein physikalischen System in einer zweidimensionalen Ebene beschreiben, nehmen wir dazu die Größen x und y. Beide müssen stets zusammen betrachtet werden, und bilden damit ein Gleichungssystem. Dies gilt sowohl für Differentialgleichungen, als auch für Differenzengleichungen und ihre schrittweisen Iterationen.

Betrachten wir dazu als einfaches Beispiel folgendes multidimensionales Differenzengleichungssystem:

x_x+1 = x + 4
y_y+1 = y - 4

Dies bedeutet, dass für jedes neue x dem alten Wert 4 hinzugefügt werden und bei jedem neuen y-Wert 4 abgezogen werden. Wenn wir nun mit einem Startwert für x und y von 20 beginnen erhalten wir für x schrittweise: 20, 24, 28, 32 ... usw. und für y entsprechend 20, 16, 12, 8 ... usw.

Beide Werte entwickeln sich dabei völlig unabhängig voneinander. Der Wert von x hat also keinerlei Auswirkung auf den Wert von y. Man spricht dann auch von einem ungekoppelten Gleichungssystem.

Betrachten wir nun jedoch einmal dieses Gleichungssystem:

x_x+1 = x + 4
y_y+1 = y - x

Nun sind beide Gleichungen miteinander verbunden, da auf der rechten Seite der zweiten Gleichung beide Variablen vorhanden sind. Der neue Wert von y hängt nun auch von dem jeweiligen Wert von x ab. Beginnen wir wieder mit einem Startwert von 20 für x und y, so erhalten wir für x erneut die Werte 20, 24, 28 ... usw., aber für y lauten die Werte dann 20, -4, -32 ... usw.

Sobald in einem Gleichungssystem mit beliebig vielen Variablen mindestens zwei Variablen miteinander interagieren, spricht man von einem gekoppelten Gleichungssystem.

Und jeder erfahrene Physiker weiß es (und jeder erfahrene Mathematiker ahnt es vermutlich): Ungekoppelte Gleichungssysteme sind geradezu unfassbar langweilig. Erst gekoppelte Gleichungssysteme führen zu den wirklich interessanten Dynamischen Systemen. Und zusammen mit der Nichtlinearität wird es dann sogar äußerst spannend bei der Erforschung des dazugehörigen Systemverhaltens.

 

Zustandsgrößen und Dimensionalität Dynamischer Systeme

Die Unterscheidung von Vorgabegrößen, Zwischengrößen und Zustandsgrößen ist für die Systemdarstellung im Zustandsraummodell von fundamentaler Bedeutung. Für jede Zustandsgröße muss dabei eine Differential- bzw. Differenzengleichung geschrieben werden.

Physikalisch betrachtet ist der Zustand eines Dynamischen Systems durch den Energiegehalt der im System vorhandenen Energiespeicher bestimmt. Die Zustandsgrößen beschreiben daher den Energiegehalt der im System enthaltenen Speicherelemente.

Die Zahl der Zustandsgrößen gibt daher die Dimensionalität des Dynamischen Systems an. Für Zwischengrößen sind lediglich algebraische Gleichungen anzugeben. Ein "eindimensionales" Dynamisches System  beispielsweise besitzt daher genau eine Zustandsgröße (unabhängig davon, wie viele physikalische Dimensionen es besitzt).

 

 

1.2 Die Analyse von Dynamischen Systemen

Umformulierung von algebraischen Gleichungssystemen höherer Ordnungen (Ableitungen)

Für die analytische Behandlung der Differential- bzw. Differenzengleichungen ist es notwendig, eventuell vorhandene algebraische Gleichungen höherer Ordnung (also beispielsweise eine zweite oder dritte Ableitung) schrittweise in Gleichungen 1. Ordnung (also erste Ableitungen) durch das Einführen neuer Zustandsgrößen umzuformen.

Zustandsraum und Übertragungsfunktion

Zum einen gibt es dafür das sog. Übertragungsmodell, welches Differentialgleichungen höherer Ordnungen, eine Übertragungsfunktion, sowie die Funktionentheorie und die komplexen Zahlen verwendet. Dort gibt es eine Ursache, eine Übertragungsfunktion, und eine Wirkung.

Zum anderen gibt es das Zustandsraummodell, welches Differentialgleichungen erster Ordnung, eine Transitionsmatrix, die Matrizenrechnung und lineare Algebra verwendet. Dort gibt es dann Eingangsgrößen, innere Größen (Zustandsgrößen), und Ausgangsgrößen.

 

 

1.3 Unterschiedliche Eigenschaften von linearen und nichtlinearen Dynamischen Systemen

Attraktoren²

Der Zustand eines dynamischen Systems verändert sich mit der Zeit. Eine Möglichkeit, diese Veränderungen zu visualisieren, besteht darin, die relevanten Variablen in einem Diagramm aufzutragen. Wenn die Zeit voranschreitet, bewegt sich der Zustand des Systems entlang eines Pfades in diesem Diagramm. Diese Pfade (Trajektorien) nehmen dann eine spezielle Gestalt an, die man Attraktor nennt. Es handelt sich dabei also um eine geometrische Beschreibung des langfristigen Verhaltens eines Systems.

Lineare Systeme besitzen nur einen einzigen Attraktor, nämlich den

• Gleichgewichtspunkt

des homogenen Systems.

Nichtlineare Systeme können hingegen unterschiedliche Attraktorarten besitzen:

• Gleichgewichtspunkt
• Grenzzyklen ("kreisförmig", Schwingungen)
• Tori (überlagerte Grenzzyklen)
• chaotische Attraktoren (nichtperiodisch)

Stabilität³

In linearen Systemen ist die Stabilität eine Systemeigenschaft. Bei nichtlinearen Systemen ist die Stabilität abhängig vom Betrag und dem Vorzeichen der Eingänge oder der Anfangsbedingungen.

Überlagerungsprinzip (Superpositionsprinzip)

Bei linearen Systemen gilt das Überlagerungsprinzip. Die Systemantwort ist die Summe der Reaktionen auf Einzelsignale. Für nichtlineare Systeme gilt das Überlagerungsprinzip nicht.

Bifurkationen: Strukturveränderung von Systemen und Katastrophentheorie

Nicht selten passiert es, das Systeme beim Erreichen bestimmter Zustandsbedingungen "umschalten" und damit ihr Verhalten qualitativ verändern. Dieses Umschalten kann etwa bedeuten, dass beim Erreichen gewisser Schwellenwerte die Parameter verändert, Verbindungen unterbrochen oder aktiviert, oder ganze Subsysteme ab- oder dazugeschaltet werden. Pflanzen oder Tiere etwa verfügen über solche Mechanismen, um Belastungssituationen überstehen zu können. 

Mit dem Begriff Bifurkation werden Phänomene beschrieben, die bei nichtlinearen, parameterabhängigen Gleichungssystemen bzw. nichtlinearen DGL-Systemen auftreten. Falls die Systemparameter geändert werden, kann für einen bestimmten Parameterwert ein plötzlicher Wechsel der Lösungsstruktur auftreten. Dann spricht man von einer Bifurkation.

Man unterscheidet dabei lokale und globale Bifurkationen.

Lokale Bifurkationen, als Bifurkationen, die nur in der Nähe ihrer Fixpunkte untersucht werden, kann man weiterhin in die Anzahl der betrachteten Kontrollparameter einteilen:

Die einfachsten Bifurkationen hängen nur von einem einzigen Kontrollparameter ab und man spricht von einer Kodimension-1-Bifurkation (Sattelknoten-Bifurkation, Hopf-Bifurkation usw.). Mit 2 Kontrollparametern, also der Kodimension-2-Bifurkation, lassen sich sowohl alle Bifurkationen der niedrigeren Klasse, als auch einige neue Bifurkationsarten behandeln, wie beispielsweise die Cusp-Bifurkation, die zum Paradigma der sogenannten mathematischen Katastrophentheorie gehört, und daher auch oft Cusp-Katastrophe genannt wird.

Ein Beispiel für eine globale Bifurkation ist die Sattle-Connection-Bifurkation.

Bifurkationen II: Attraktoren vs. Attraktoren

Bei lokalen Bifurkationen kollidieren Attraktoren bzw. Repelloren durch die Veränderung von Parametern und das System verändert seine Stabilität in der Nähe des Fixpunktes.

Bei globalen Bifurkationen kollidieren ganze Sets von Attraktoren, wie beispielsweise ein Grenzzyklus mit einem Gleichgewichtszustand, wie beispielsweise einem Sattelpunkt-Attraktor.

 

 

1.4 Konservative Systeme

Konservative Dynamische Systeme sind Systeme, in denen die Energie erhalten bleibt. Dazu gehören beispielsweise alle mechanischen Systeme ohne Reibung, oder alle elektrischen Schaltkreise ohne ohmschen Widerstand.

Man untersucht hier innerhalb der analytischen Mechanik vor allem Fragen der Integrabilität und das Verhalten im Phasenraum.

Es gilt bei konservativen Systemen stets der Satz von Liouville, der besagt: Die Größe der Fläche, die ein Ensemble im Phasenraum einnimmt, verändert sich nicht im Laufe der Zeitentwicklung des Systems. Damit wird dem System eine große Beschränkung auferlegt. Die Form der Fläche mag variieren, und für nichtlineare Systeme sogar zu einem Fraktal werden, aber der Flächeninhalt bleibt immer gleich.

Hamiltonische Systeme

Hamiltonische Systeme sind einer spezielle Klasse von konservativen Systemen. Untersucht werden hier die Fragen zur Integrabilität und Stabilität eines Systems.

Integrable Systeme

Um die Bewegungsgleichung eines gegebenen dynamischen Systems zu integrieren, versucht man solche Koordinaten zu finden, in denen das System harmonische Schwingungen ausführt. Dabei stellt sich die Frage, ob durch eine geeignete Koordinatentransformation ein konservatives System auf einen oder mehrere gekoppelte harmonische Oszillatoren zurückgeführt werden kann. Ein integrables System liegt genau dann vor, wenn es bei geeigneter Wahl der Variablen als Überlagerung harmonischer Oszillatoren beschrieben werden kann.

Damit beruht die Definition eines integrablen Systems auf der Möglichkeit, Wechselwirkungen zwischen Teilchen zu eliminieren, so dass man zu einem einfachen System freier Teilchen gelangt.

Alle eindimensionalen Systeme und alle linearen Systeme sind beispielsweise integrabel. Das Zwei-Körper-Problen (ein Planet kreist um die Sonne) ist integrabel. Das Drei-Körper-Problem (zwei Planeten kreisen um die Sonne) ist jedoch nichtintegrabel. Es existieren bestimmte stabile Orbits, andere Orbits sind unstabil und führen zum Entweichen des Planeten von seiner Bahn und/oder zum Zusammenbruch des Systems.

Nichtintegrable Systeme und Ergodentheorie

Bis zum Ende des 19. Jahrhunderts nahm man an, dass alle Dynamischen Systeme integrabel seien. Heutzutage zeigt die analytische Mechanik, dass die überwältigende Mehrheit der Systeme jedoch nichtintegrabel ist und integrable Systeme nur einen Sonderfall darstellen. Als Erster hatte Poincare diese Behauptung mathematisch untersucht, und auch den Grund dafür genannt: die Existenz von Resonanzen zwischen den Freiheitsgraden, denn Resonanzen bewirken eine starke Kopplung zwischen den Freiheitsgraden. Und gekoppelte Freiheitsgrade sind nun gerade nicht mehr unabhängig voneinander, und lassen sich daher dann auch nicht mehr wie freie Teilchen behandeln. 

Nichtintegrable Systeme zeigen das Verhalten von deterministischem Chaos. Jedes System mit mehr als einem Freiheitsgrad kann dabei unter gewissen Umständen chaotisches Verhalten entwickeln.

Das Langzeitverhalten von nichtintegrablen Systemen wird u. a. im Rahmen der Ergodentheorie untersucht. Dabei werden statistische Eigenschaften ermittelt, die zeigen, inwiefern ein System in der Lage ist, den gesamten Phasenraum zu durchstreifen, oder auch nicht. Das Gegenteil von ergodischem Verhalten stellen daher alle integrablen Systeme dar. Sie belegen nur einen winzig kleinen Ausschnitt des Phasenraums. 

 

 

1.5 Dissipative Systeme

Dissipative Systeme sind Systeme, in denen die Energie nicht erhalten bleibt, sondern sie innerhalb der Dynamik verloren geht, und damit in die Umwelt gestreut (dissipiert) wird. Dissipative Systeme sind daher immer offene Systeme, die Energie aus der Umwelt aufnehmen, und auch wieder abgeben können. Ohne ständige Energiezufuhr hören die entsprechenden Systeme auf zu existieren.

Untersucht wird hier vor allem das Langzeitverhalten, welches zu verschiedenartigster Attraktorbildung führt. U. a. beobachtet man im chaotischen Bereich eine Empfindlichkeit gegenüber den Anfangsbedingungen und die Ausbildung sogenannter "seltsamer Attraktoren", die durch ihre Irregularität trotz vollständigem Determinismus gekennzeichnet sind.

Zu diesen Systemen gehört beispielsweise ein Pendel mit einer Dämpfung, alle reibungsbehafteten mechanischen Systeme, sowie elektrische Schaltkreise mit einem ohmschen Widerstand.

Für dissipative Systeme gilt der Satz von Liouville nicht. In einem dissipativen System verringert sich die Größe der Fläche, die ein Ensemble im Phasenraum einnimmt, im Laufe der Zeitentwicklung des Systems. Charakteristisch für dissipative Systeme ist die Existenz von Attraktoren und Grenzzyklen, die ihr Langzeitverhalten bestimmen. 

Attraktoren: Fixpunkt, Grenzzyklus und seltsame Attraktoren

Ein Attraktor ist ein Zustand, in den ein dissipatives System quasi "hineinläuft", so als ob es von ihm "angezogen" wird. Wegen des Satzes von Liouville ist dies in konservativen Systemen nicht möglich. In dissipativen Systemen macht aber gerade die Untersuchung der möglichen Formen von Attraktoren einen Großteil der Analyse des Systemverhaltens aus.

Ein Attraktor ist ein Bereich im Phasenraum, den das System, wenn es ihn einmal erreicht hat, nicht mehr verlassen wird. Bei einem Fixpunktattraktor besteht dieser Zustand aus genau einem einzigen, fixen Punkt im Phasenraum. Weiterhin gibt es auch periodische Gebiete, von denen ein dissipatives System angezogen wird. Von ganz unterschiedlichen Anfangsbedingungen aus geht dann die Systemdynamik in einen periodischen Zustand über, wie beispielsweise einer konstanten Schwingung. Neben regulären Orbits kann ein dissipatives System jedoch auch zu konstantem irregulären Verhalten übergehen. Man spricht dann von einem seltsamen Attraktor, der dadurch gekennzeichnet ist, dass die Trajektorien auch auf lange Zeit keine Wiederholungen erkennen lassen, und zudem eine starke Empfindlichkeit hinsichtlich der Anfangsbedingungen zeigen. Dann liegt ein deterministisches chaotisches System vor.

 

 

1.6 Ausblick: Die spannende strukturwissenschaftliche Erforschung nichtlinearer Systeme

Die Entwicklung der klassischen, nichtrelativistischen, linearen analytischen Mechanik kann heute als weitgehend abgeschlossen betrachtet werden. Ihre Prinzipien haben sich in der Physik bewährt.

Historisch betrachtet findet die lineare analytische Mechanik einen gewissen Endpunkt mit dem Noether-Theorem von 1918, das einen sehr allgemeinen Zusammenhang zwischen Symmetrien und Erhaltungsgrößen herstellt. Dabei hatte sich die Mechanik bereits von der ursprünglichen Newtonschen Mechanik zur Lagrangeschen Mechanik weiterentwickelt.

Die darauf folgende Hamiltonische Mechanik stieß dann das Tor für die Untersuchungen im Rahmen der statistischen Physik und der nichtlinearen Dynamik auf. Die nichtlineare Dynamik und die Erforschung chaotischer Bewegungsformen erweitert dabei das Gebäude der Mechanik so stark, dass man schon fast von einem eigenständigen Zweig der neuzeitlichen Mechanik sprechen könnte. 

Denn es zeigte sich schnell (siehe u. a. das KAM-Theorem), dass in der Natur die klassische stabile, reguläre Bewegung eine Ausnahme darstellt und fast nie in reiner Form zu finden ist. Die klassischen Systeme sind in ihrer Dynamik zudem äußerst langweilig, und beschreiben entweder das Vorhandensein eines fixen, stabilen Punktes, oder das stabile oszillieren im Rahmen eines sich ständig wiederholenden Zyklus.

Lange Zeit beherrschte diese Sichtweise auch die Einstellung in Bezug auf die Evolution der Natur als Ganzes. D.h. entweder würde alles auf einen festen Endpunkt hinstreben, oder sich in endlosen Schleifen auf ewig wiederholen. Die moderne Mechanik zeigt dagegen den Weg einer komplexen Evolutionskette auf, die es uns ermöglicht, auch progressive strukturbildende Mechanismen aufzudecken, welche stets vielfältigste neue und überraschende Systeme bzw. Systemverhalten generieren können.

Diese kreative und teilweise auch prinzipiell unvorhersehbare Evolution ist ein Modell, dass viel besser in unser Bild von der Natur und ihre knapp 14 Milliarden Jahre andauernde Evolution beschreibt. Seit dem Urknall haben es diverse komplexe strukturbildende Maßnahmen ermöglicht, schließlich sogar Lebewesen hervorzubringen.

Die schrittweise Aufdeckung der zugrundeliegenden Mechanismen ist ein spannendes Gebiet strukturwissenschaftlicher Forschung, da im Bereich der nichtlinearen Dynamischen Systeme noch kein geschlossenes strukturwissenschaftliches Theoriegebäude existiert. Manch einer mag daher bei der Beschäftigung mit komplexen Systemen von der Vielfalt möglicher Theoriegebäude eher abgeschreckt oder verwirrt werden. Doch genau an solchen Stellen ist die Forschen auch ganz besonders lohnenswert und spannend.

 

 

 

 

2. Die Systemdynamik elementarer Dynamischer Systeme

 

 

2.1 Systemdynamik 0: Statische, speicherlose Systeme

Bildlizenz-Info: Bild selbst erstellt mit Excel, Public Domain

Nulldimensionale Dynamische Systeme

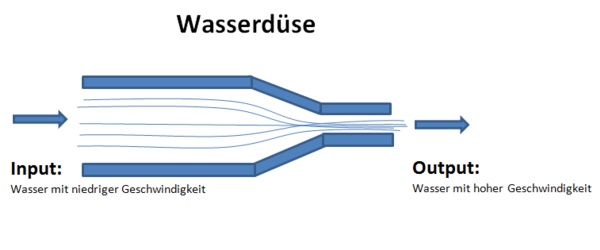
Betrachten wir nun das lineare oder nichtlineare speicherlose System, welches nulldimensional genannt wird, da es keine einzige Zustandsgröße besitzt.

Das System enthält lediglich Vorgabewerte und Zwischengrößen. In einem speicherlosen System werden Eingangsgrößen durch algebraische oder logische Anweisungen direkt transformiert.

Die Entwicklungsgeschichte hat dabei keinerlei Einfluss auf das augenblickliche Verhalten. Ein solches System ist daher nur ein Wandler bzw. ein Transformator.

Diese Systeme sind ausschließlich exogen bestimmt. Aus Sicht der Kausalität liegt hier eine lineare Kausalität vor, d.h. eine Einwirkung führt direkt zu einer Auswirkung. In der Kybernetik nennt man solch ein System daher auch eine "triviale Maschine".

 

 

2.2 Systemdynamik I: Systeme mit einer Zustandsgröße

Bildlizenz-Info: Bild selbst erstellt mit Excel, Public Domain

Eindimensionale Dynamische Systeme

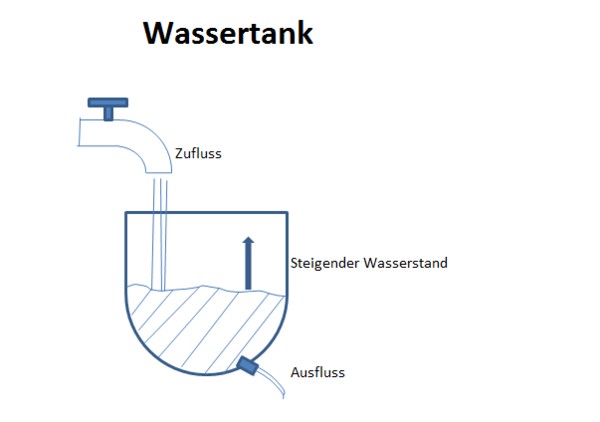
Die nächste Stufe sind die zustandsbestimmten Systeme, die mindestens eine Zustandsgröße besitzen, und daher eindimensionale dynamische Systeme genannt werden.

Zustandsbestimmte Systeme können sich auch dann verändern, wenn überhaupt kein äußerer Einfluss vorliegt. Daher herrscht dann keine einfache Ursache-Wirkungsbeziehung vor, da gleiche Einwirkungen zu unterschiedlichen Auswirkungen führen können. Im einfachsten Falle des eindimensionalen Systems ergibt sich durch die Rückkopplung einer einzigen Zustandsgröße mit sich selbst eine Zustandsänderung. Hier hängt daher die Zustandsveränderung vom Zustand des Systems selbst ab.

Für das dargestellte Beispiel des Wassertanks bedeutet dies, dass beispielsweise aus dem Ausfluss aufgrund der Speicherung auch dann einige Zeit lang Wasser fließt, wenn keinerlei Zufluss von Außen erfolgt. Auch wird bei steigender Wasserstandshöhe der Wasserdruck auf den Ausfluss immer größer, und die Ausflussgeschwindigkeit steigt, obwohl der Zufluss konstant bleibt.

In der Kybernetik nennt man Systeme mit mindestens einem internen und variablen Zustand auch "nicht-triviale Maschine".

Sehen wir uns dazu zusätzlich noch für das einfachste eindimensionale dynamische System die Modellierung des Systemdiagramms (System Dynamics) und die zugehörigen Rechenergebnisse an: 

                
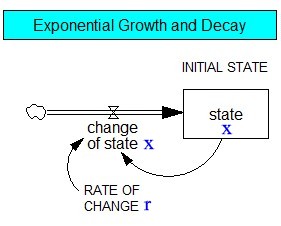
Bildlizenz-Info: Bilder selbst erstellt mit Vensim und Excel, Public Domain

Dabei beschreibt die lineare Zustandsgleichung

dx/dt = r x

ein Wachstum oder einen Schwund, je nach Vorzeichen der Parameter.

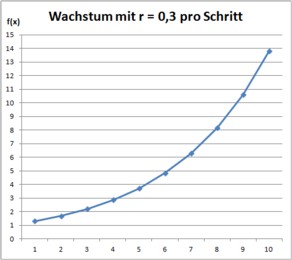
Ist r = 0,3, dann wächst diese Größe mit jedem Wachstumsschritt um den Faktor 1,3. Im ersten Wachstums-Schritt erhalten wir aus dem Startwert von 1 mit 1 mal 1,3 den Wert 1,3. Im zweiten Schritt dann 1,3 mal 1,3 also 1,69 usw. ...

Das Excel-Diagramm zeigt auf der x-Achse die Zeit und auf der y-Achse die Größe von x bzw. das Wachstum. Trotz der linearen Gleichung ergibt sich hier ausnahmsweise einmal ein "nichtlinearer" Graph als exponentiell ansteigende Kurve.

Im linken Systemdiagramm erkennt man gut, wie die eine Zustandsgröße x (Kästchen "state x") auf sich selbst zurückwirkt und damit ihre eigene Veränderung steuert.

 

 

2.3 Systemdynamik II: Schwingungsfähige Systeme

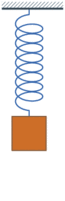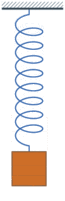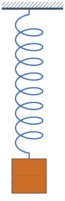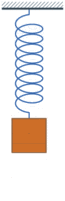
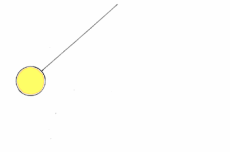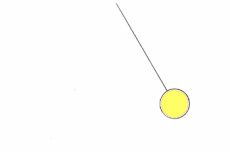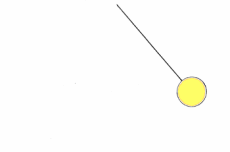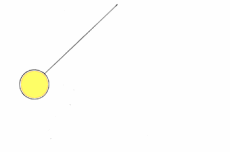
Bildlizenz-Info: simple harmonic oscillator, Wikipedia, Public Domain und nichtlineares einfaches Pendel

Zweidimensionale dynamische Systeme

Die Grundstruktur der in den Animationen dargestellten, zweidimensionalen dynamischen Systeme, besteht im einfachsten Falle aus zwei Zustandsgrößen, die miteinander verkoppelt sind und somit in eine gegenseitige Wechselwirkung treten können. Die Größe A beeinflusst die Größe B und die Größe von B beeinflusst die Größe A. Ein solches System besitzt die Neigung, bei einer konstanten Frequenz zu schwingen.

Wenn also der Zustand die Veränderungsrate einer zweiten Zustandsgröße bestimmt und diese wiederum die Veränderungsrate der ersten, so haben wir eine über zwei Zustandsgrößen laufende Rückkopplung. Ist dieser Rückkopplungskreis negativ, kann das System schwingen. Beim Feder-Masse-System bewirkt eine Auslenkung x eine entgegengesetzte Rückstellkraft und damit eine negative Rückkopplung.

Bei diesem  Klassiker der Dynamischen Systeme handelt es sich um sogenannten linearen Schwinger. Sie zeichnen sich durch eine extrem gute Berechenbarkeit aus, und auch das langfristige Systemverhalten ist beliebig genau bestimmbar.

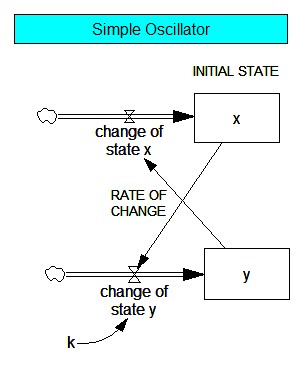
Bildlizenz-Info: Bild selbst erstellt mit Vensim, Public Domain

Wenn wir k als Federkonstante annehmen und y als Geschwindigkeit der Masse, dann entspricht das System einem harmonischen Schwinger mit der Kopplungsstärke k und den Zustandsgleichungen

dx/dt = y
dy/dt = - k x

Wir erkennen hier die zwei Zustandsgrößen x und y, die beide nur in der ersten Potenz vorkommen. Man spricht daher von einem zweidimensionalen linearen dynamischen System. Die Feder ist dabei der (lineare) Speicher für die potentielle Energie, und die Masse ist der Speicher für die kinetische Energie.

Im ungedämpften System wird sich hier eine Schwingung mit einer festen Frequenz einstellen, bei einer gedämpften Schwingung strebt das System dem stabilen Gleichgewicht ohne Auslenkung oder Bewegung zu.

Wichtig für die Systemdynamik ist jedoch, dass ein schwingungsfähiges System mindestens zwei Zustandsgrößen aufweisen muss. Auch Systeme mit drei und mehr Freiheitsgraden können im linearen Falle schwingen. Doch ab drei Freiheitsgraden gibt es auch noch weitere Möglichkeiten der Systemdynamik, welche in den folgenden Kapiteln behandelt werden.

 

 

2.4 Systemdynamik III: Chaostheorie und deterministisches Chaos

Bildlizenz-Info: Double compound pendulum, Wikipedia, Public Domain

Dreidimensionale, nichtlineare Dynamische Systeme

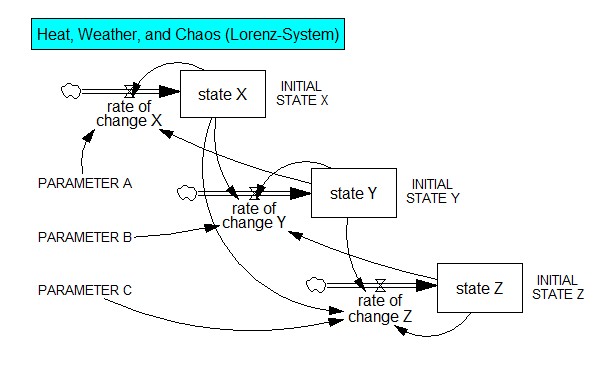
Bildlizenz-Info: Bild selbst erstellt mit Vensim, Public Domain

Auf dem Bild sehen wir das Systemdiagramm des berühmten Lorenz-Systems. In diesem simplen nichtlinearen Gleichungssystem, das ursprünglich zur Wettervorhersage erstellt wurde, befinden sich die drei miteinander verkoppelten Zustandsgrößen X, Y und Z, und die Parameter A, B und C. Es gilt dabei folgendes Gleichungssystem:

dX/dt = -A(X-Y)

dY/dt = BX-Y-XZ

dZ/dt = XY-CZ  

Die Nichtlinearität "versteckt" sich in diesem Gleichungssystem ein wenig, und zwar in der dritten Gleichung, in der der Term X*Y steht. Da nun aber die Gleichungen für X und Y ebenfalls wieder die Faktoren X und Y erhalten, wird die Multiplikation nichtlinear.

Trotz dieser mathematisch recht einfachen Struktur, zeigt das Gleichungssystem ein erstaunlich reichhaltiges Lösungsverhalten. Die Entwicklung hin zum chaotischen System kann man dabei schrittweise durch die Erhöhung eines Kontrollparameters verfolgen und analysieren:

Fixieren wir dazu den Parameter A beim Wert 10 und den Parameter C bei 8/3 und variieren nun lediglich den Parameter B. Wird der Kontrollparameter B größer als 1, erfolgt eine erste Gabelverzweigung. Ab dem Wert 13,92 tritt eine globale Bifurkation ein. Das deterministische Chaos erscheint per subkritischer Hopf-Verzweigung bei 24,74. Die drei Gleichgewichtspunkte der Eigenwerte führen dann ein Wechselspiel aus stabilem und instabilem Verhalten aus und die Trajektorie wird dauerhaft irregulär. Doch auch im Lorenz-System finden wir bei höheren Parameterwerten ab und zu wieder periodische Orbits, wie beispielsweise beim Wert 100,5. Auch diese "Inseln der Ordnung" sind daher typisch für das chaotische Systemverhalten.   

 

2.4.1 Bedingungen für chaosfähige Systeme:⁸

• das System muss nichtlinear sein
• es muss eine Stelle sensitiver Abhängigkeit von den Anfangsbedingungen existieren (beispielsweise durch ein W-Potential)
• es muss mindestens drei (effektive) Freiheitsgrade haben

Die Rolle der Nichtlinearität

Nichtlinearität ist eine notwendige, aber nicht hinreichende Bedingung sowohl für das Entstehen von ‚Chaos aus Ordnung‘ (Deterministisches Chaos), als auch für die Entstehung von ‚Ordnung aus Chaos‘ (Selbstorganisation und Synergetik). Sie bewirkt einmal das Stolpern eines angetriebenen nichtlinearen Oszillators oder einer Reihe gekoppelter nichtlinearer Oszillatoren, d. h., dass diese aus dem Tritt geraten. Die Frequenz ist dann im Gegensatz zu linearen Oszillatoren nicht mehr amplitudenunabhängig. Es gilt nicht mehr das additive Superpositionsprinzip, wie für lineare Schwingungen. Demzufolge können bei nichtlinearen Schwingern neue Kombinationsfrequenzen entstehen, wenn sie periodisch mit verschiedenen Frequenzen angetrieben werden.

Umgekehrt sind nichtlineare Systeme leichter zu synchronisieren als lineare Systeme. Durch die Kopplung zwischen Auslenkung und Frequenz kann das Schwingungssystem flexibler auf äußere Kräfte reagieren. Das additive Superpositionsprinzip ist nämlich durch das multiplikative Ähnlichkeitsprinzip ersetzt: Eine Änderung der Längenskala ist mit einer entsprechenden Änderung der Zeitskala verbunden. Durch Phasenkopplung benachbarter Frequenzkomponenten können spektrale Anteile verschwinden, d. h., das System synchronisiert sich. Es kommt zu synergetischen Effekten.

Die Rolle der Sensitivität

(Kubische) Nichtlinearitäten geben dem Potenzial eine W-Form. Durch die Existenz zweier Potenzialmulden vermag das System chaotisch zwischen beiden hin und her zu springen. Im Bereich des Potenzialwalls ist das System hochsensitiv.

Die Rolle des 3. Freiheitsgrades

Der 3. Freiheitsgrad ist ebenfalls sowohl für das Entstehen von ‚Chaos aus Ordnung‘ (Deterministisches Chaos), als auch für die Entstehung von ‚Ordnung aus Chaos‘ (Selbstorganisation und Synergetik) bedeutsam. Für das deterministische Chaos ist der 3. Freiheitsgrad deswegen so wichtig, da der Determinismus es verbietet, dass sich Trajektorien im Phasenraum schneiden (Kreuzungsverbot). Ansonsten wären die Lösungen der Bewegungsgleichungen nicht eindeutig.

Der dritte Freiheitsgrad hat bei angetriebenen nichtlinearen Oszillatoren im Phasenraum noch eine topologische Folge: die Rückfaltung im Phasenraum.

Beispiel Doppelpendel (siehe oben): Das Doppelpendel besitzt 2 Orts- und 2 Geschwindigkeitsvariablen. Dies entspricht zunächst 4 Freiheitsgraden. Dann muss man jedoch einen Freiheitsgrad wieder abziehen, da eine Kopplung über den Energieerhaltungssatz besteht. Das macht dann in Summe genau die geforderten mindestens drei effektiven Freiheitsgrade.

Nach A. Pflug⁹ kann der Übergang von Ordnung zu Chaos anhand der Freiheitsgrade grundsätzlich in drei Klassen unterteilt werden, die sich anhand der Anzahl der effektiven Freiheitsgrade ergeben:

• <= 2 Ordnung
• 3....100 Chaos und Ordnung
• 100 Dominanz von Chaos

 

2.4.2 Beispiele einfacher chaosfähiger Systeme 

Dimensionsreduzierte dynamische Systeme

• Logistische Abbildung (Logistic Map)
• Standard-Abbildung (Standard-Map)
• Henon-Abbildung

Dreidimensionale dynamische Systeme

• Lorenz-System
• Rössler-System
• Doppelpendel
• Magnetpendel mit drei Magneten
• Dreikörperproblem

 

 

2.5 Systemdynamik IV: Selbstorganisation

Als Selbstorganisation wird in der Systemtheorie hauptsächlich eine Form der Systementwicklung bezeichnet, bei der die formgebenden, gestaltenden und beschränkenden Einflüsse von den Elementen des sich organisierenden Systems selbst ausgehen.

Um von Selbstorganisation sprechen zu können, müssen folgende Kriterien erfüllt sein:

• Die Evolution eines Systems in eine räumlich/zeitlich organisierte Struktur ohne äußeres Zutun
• Die autonome Bewegung in immer kleinere Regionen des Phasenraumes (die Attraktoren)
• Die Entwicklung von Korrelationen oder raumzeitlichen Mustern zwischen vorher unabhängigen Variablen, deren Entwicklung nur unter dem Einfluss lokaler Regeln

 

 

2.6 Systemdynamik V: Zufällige Dynamik und Random Walk

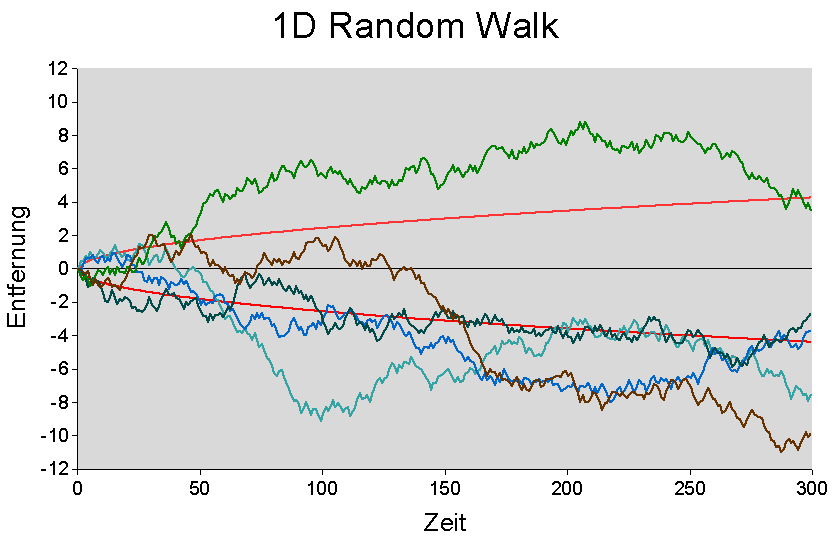
Bildlizenz-Info: Quelle Wikipedia, Random Walk, Public Domain

Wichtig zu erwähnen ist zunächst, dass die zufällige Systemdynamik nicht nur nicht deterministisch ist, sondern sogar per se nicht berechenbar ist. Es hat keinen Sinn nach einem Algorithmus zu fragen, wenn es keinen gibt, da keinerlei Zusammenhänge (Relationen) zwischen den Ereignissen bestehen.

Trotzdem kann man sich auch der Zufallsdynamik im Rahmen der Stochastik annähern. Wahrscheinlichkeitsverteilungen bestimmen dann zumindest den Trend einer zufälligen Dynamik. Der konkrete Einzelfall bzw. das Einzelereignis bleibt jedoch prinzipiell unberechenbar.

Markov-Ketten

Bei Markov-Ketten handelt es sich um eindimensionale Aneinanderreihungen von Zufallsereignissen, die sowohl diskret in der Zeit, als auch in den Zuständen sind. Es werden dabei meist nur recht wenige mögliche Zustände (Zufallsvariablen) betrachtet und deren Übergangswahrscheinlichkeiten definiert. So kann man beispielsweise die Ergebnisse von Würfen mit einem Würfel aneinanderreihen. Dort hat man 6 mögliche Zustände, und die Übergangswahrscheinlichkeit liegt immer bei 1/6 (inklusive der Wahrscheinlichkeit, die gleiche Zahl noch einmal zu würfeln).

Random Walk

Das Wort "Random Walk" kommt aus dem Englischen und bedeutet Zufallsbewegung. Die wesentliche Eigenschaft eines Random Walk ist die Unabhängigkeit der einzelnen Schritte. Jede weitere Verschiebung des "Walkers" hängt nur von seiner momentanen Lage (Gegenwart) und nicht von den bereits besuchten Plätzen (Vergangenheit) ab. Im Gegensatz zu Markov-Ketten besitzt der Random Walk jedoch keinerlei Beschränkung hinsichtlich der Zufallsvariablen, daher besitzt er potentiell unendlich viele verschiedene mögliche Zustände.

Ein Beispiel für einen 1-dimensionalen  Random Walk ist ein Spielstein auf einer Geraden, auf der er jeweils ein Stück weit nach links oder rechts gehen kann. In welche Richtung sich der Spielstein bewegt, ist dabei rein zufällig. Man kann sie zum Beispiel durch eine Münze bestimmen, die vor jedem Zug neu geworfen wird.

Bei einem zweidimensionalen Random Walk kann der Spielstein dann sowohl nach rechts oder links, oder auch nach oben oder unten verzweigen.

 

 

2.7 Systemdynamik VI: Die Evolution von komplexen dynamischen Systemen

Das basale Konzept der Evolution, nämlich die Veränderung im Laufe der Zeit, spielt auch für elementare dynamische Systeme eine überragende Rolle. Anfänglich war auch gerade sie es, die überhaupt die Beschäftigung mit komplexen Systemen motivierte, denn man versuchte (ausgehend von der klassischen Mechanik) das Langzeitverhalten der Planetenbewegungen in Bezug auf deren Stabilität analysieren.

Es mag überraschen, dass bereits bei so simplen Systemen mit nur drei Freiheitsgraden eine derart vielfältige Systemevolution überhaupt möglich ist, die von nichtintegrablen Systemen bis zu seltsamen Attraktoren oder spontanen Synchronisations- und Organisationsphänomenen reicht. Eine analytische Lösung der nichtlinearen Fällen ist in den allermeisten Fällen nicht möglich, so dass man hier auf Computersimulationen zurückgreifen muss. Interessant ist auch, dass es in Abhängigkeit von den eingestellten Kontrollparametern nicht nur zur vielfältigen Evolutionsvarianten kommt, sondern das diese dabei sogar von ein und demselben System stammen.

An die faszinierenden Leistungen etwa der biologischen Evolution reichen diese einfachen Elementarsysteme zwar bei weiten noch nicht heran, aber sie liefern immerhin bereist einen Vorgeschmack darauf, was den Forscher bei noch komplexeren Systemen wohl noch so alles erwarten mag.

 

 

 

 

3. Räumlich ausgedehnte Systeme: Struktur- und Musterbildung in komplexen Netzwerken

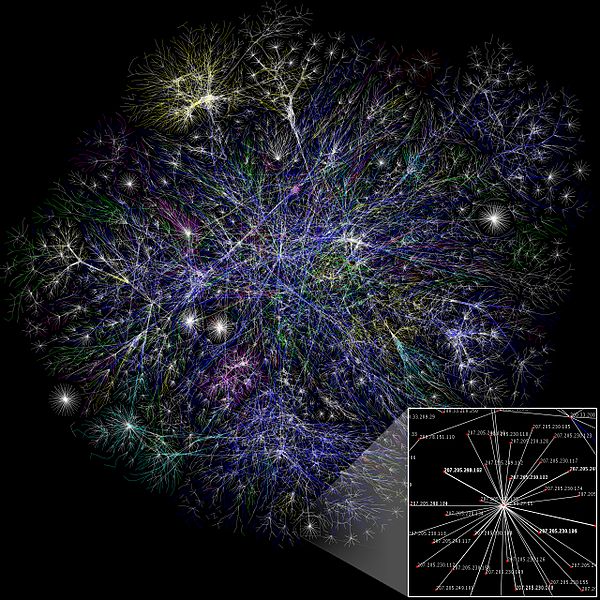
Bildlizenz-Info: Internet map 1024, Wikipedia, Complex network, Public Domain

Im vorherigen Kapitel wurden einfache und etwas komplexere Systeme hauptsächlich deshalb aufgebaut, um ihre zeitliche Dynamik untersuchen zu können.

Die räumliche Anordnung, ja selbst die räumliche Ausdehnung des Systems spielte dabei keine Rolle. Abstrakt gesehen könnte man sich solch ein System von Außen auch als eine "Black Box" vorstellen, die in einem kleinen Punkt im Raum irgendwo vorhanden ist. Solange dieser Punkt nur die gewünschte Systemdynamik zeigt, ist alles in Ordnung.

Nun spricht aber nichts dagegen, eine ganze Menge einzelne Systeme im Raum gezielt anzuordnen, und schrittweise miteinander zu verbinden, sprich zu vernetzen. Solche räumlich ausgedehnten Systeme sind die Weiterentwicklung von Einzelsystemen und dabei werden die aus der Summe der Systeme resultierenden Eigenschaften dann jedoch stark von der Anordnung im Raum und der jeweiligen Vernetzungsstruktur beeinflusst.

Und als komplexe Weiterentwicklung der Möglichkeiten von Einzelsystemen treten nun auch ganz neue Eigenschaften auf, zu denen beispielsweise auch die spontane Musterbildung quasi "aus dem Nichts" gehört. Diese und weitere wichtige Eigenschaften sind im folgenden Kapitel genauer beschrieben.

 

 

3.1 Wichtige Eigenschaften komplexer dynamischer Netzwerke

 

Autopoiesis

Autopoiesis oder Autopoiese ist der Prozess der Selbsterschaffung und -erhaltung eines Systems.

In der Biologie stellt das Konzept der Autopoiesis einen Versuch dar, das charakteristische Organisationsmerkmal von Lebewesen oder lebenden Systemen mit den Mitteln der Systemtheorie zu definieren. Der vom chilenischen Neurobiologen Humberto Maturana geprägte Begriff wurde in der Folge seiner Veröffentlichungen aufgebrochen und für verschiedene andere Gebiete abgewandelt und fruchtbar gemacht.

Autopoietische Systeme (beispielsweise Menschen und andere Säugetiere) sind rekursiv organisiert, das heißt das Produkt des funktionalen Zusammenwirkens ihrer Bestandteile ist genau jene Organisation, die diese Bestandteile produziert. Durch diese besondere Form der Organisation lassen sich lebende von nicht-lebenden Systemen unterscheiden: nämlich dadurch, dass das Produkt ihrer Organisation sie selbst sind, das heißt, es gibt keine Trennung zwischen Erzeuger und Erzeugnis. Das Sein und das Tun einer autopoietischen Einheit sind untrennbar, und dies bildet ihre spezifische Art von Organisation.

 

Selbstorganisation

Als Selbstorganisation wird in der Systemtheorie hauptsächlich eine Form der Systementwicklung bezeichnet, bei der die formgebenden, gestaltenden und beschränkenden Einflüsse von den Elementen des sich organisierenden Systems selbst ausgehen.

Selbstorganisation ist das spontane Auftreten neuer, stabiler, effizient erscheinender Strukturen und Verhaltensweisen (Musterbildung) in offenen Systemen. Das sind Systeme, die sich fern vom thermodynamischen Gleichgewicht befinden, die also Energie, Stoffe oder Informationen mit der Außenwelt austauschen. Ein selbstorganisiertes System verändert seine grundlegende Struktur als Funktion seiner Erfahrung und seiner Umwelt. Die interagierenden Teilnehmer (Systemkomponenten, Agenten) handeln nach einfachen Regeln und erschaffen dabei aus Chaos Ordnung, ohne eine Vision von der gesamten Entwicklung haben zu müssen. Ein einfacher Fall von (physikalischer) Selbstorganisation ist z. B. das Auftreten von Konvektionszellen beim Erhitzen von Flüssigkeiten (Bénard-Experiment).

Diese offenen Systeme fern vom thermodynamischen Gleichgewicht stehen in permanentem Kontakt mit ihrer Umwelt, von der ständig Energie zur Aufrechterhaltung der Ordnung zugeführt wird. Unterbleibt die Energiezufuhr, so gehen die Systeme gemäß dem zweiten Hauptsatz der Thermodynamik in den Zustand größter Unordnung über, und die regelmäßigen Muster verschwinden zugunsten eines letztlich stationären, homogenen Zustands, das System befindet sich im Gleichgewicht. Durch Zuführen von Energie besteht die Möglichkeit, die Systeme von außen zu steuern. Man ordnet den Steuermechanismen Kontrollparameter zu, die die Emergenz qualitativ verschiedener Ordnungszustände bewirken können. Die Kontrollparameter sind jedoch zeitlich konstant und geben in keinem Fall die auftretenden zeitlich und/oder räumlich variierenden Muster vor. Die Bildung der verschiedene geordneten Strukturen wird nicht von außen geprägt, sondern entsteht durch Selbstorganisation, also von innen.

Eine weitere Gemeinsamkeit der genannten Phänomene besteht darin, da die jeweiligen Systeme, sofern sie einer mathematisch quantitativen Beschreibung überhaupt zugänglich sind, nur durch sehr komplizierte Gleichungen erfassbar sind, die sich in den wenigsten Fällen exakt lösen lassen. Diese Gleichungen beschreiben die interessierende Strukturbildung, darüber hinaus aber auch noch eine Fülle von weiteren Verzweigungen und Effekten, die in Zusammenhang mit der zu untersuchenden Ordnungsbildung keine Rolle spielen. Man strebt daher eine einheitliche Beschreibung selbstorganisierender Systeme an, um zu einem besseren theoretischen Verständnis der gemeinsamen Eigenschaften dieser Systeme zu gelangen (Haken, Prigogine).

Es lässt sich zeigen, dass sich selbstorganisierende Systeme tatsächlich in der Nähe von Phasenübergängen nur durch wenige Größen, den Ordnungsparametern, quantitativ beschreiben lassen, für welche universelle, den Phasenübergang charakterisierende Ordnungsparametergleichungen gelten. Es gibt systematische Methoden, wie man diese wenige Ordnungsparametergleichungen aus den komplexen Grundgleichungen herleiten, und dabei die meisten der sehr vielen dynamischen Freiheitsgrade des Systems durch die Ordnungsparameter eindeutig ausdrücken und damit eliminieren kann. Die universellen Prinzipien, die zur Selbstorganisation führen, können dann anhand der Ordnungsparametergleichungen mathematisch analysiert werden (Bestehorn, 1995).

   Weblink: Selforganisation at Scholarpedia online

 

Synergetik

Ein mathematisch gut ausgearbeitet Konzept für die Selbstorganisation durch Ordnungsparameter ist die Theorie der Synergetik (Haken). Ursprünglich diente sie der Beschreibung der Selbstorganisationsphänomene bei der Entstehung von Laserlicht. Doch das theoretische Grundkonzept kann auch auch vielerlei andere Bereiche übertragen werden, wie beispielsweise bei der Beschreibung der Wolkenbilung.

   Weblink: Synergetics at Scholapedia online

 

Dissipative Strukturen - Strukturbildung in offenen Systemen

Mit dem Begriff Dissipative Struktur (engl. dissipative structure ‚zerstreuende Struktur‘) wird das Phänomen sich selbstorganisierender, dynamischer, geordneter Strukturen in nichtlinearen Systemen fern des thermodynamischen Gleichgewichts bezeichnet. Dissipative Strukturen bilden sich nur in offenen Nichtgleichgewichtssystemen, die Energie, Materie oder beides mit ihrer Umgebung austauschen. Beim Aufbau geordneter Strukturen nimmt die Entropie (Unordnung) lokal ab; diese Entropieminderung des Systems muss durch einen entsprechenden Austausch mit der Umgebung ausgeglichen werden.

Die Ausprägung geordneter Strukturen hängt entscheidend von den Systemparametern ab, wobei der Übergang vom ungeordneten zum geordneten Zustand sprunghaft erfolgt. Dissipative Strukturen zeigen eine gewisse Stabilität gegenüber Störungen von außen, zerfallen jedoch, sobald der Austausch mit der Umgebung unterbrochen wird oder allgemein bei größeren Störungen der Systemparameter.

Bereits ab 1950 arbeitete Alan Turing an einer neuen mathematischen Theorie der Morphogenese, welche die Auswirkungen nichtlinearer chemischer Reaktions- und Diffusionsfunktionen auf spontane Strukturbildungen zeigt. Die Ergebnisse dieser Arbeit hat er 1952 unter dem Titel „The chemical basis of morphogenesis“ veröffentlicht. Diese Arbeit (Turing-Mechanismus) wird als wegweisend für die spätere Entdeckung dissipativer Strukturen angesehen.

Der Begriff "Dissipative Struktur" selbst wurde 1967 vom Physikochemiker Ilya Prigogine vorgeschlagen, der ab den 1940er Jahren an der Entwicklung der Theorie der Nichtgleichgewichtsthermodynamik beteiligt war. Prigogine untersuchte die Kinetik von offenen Systemen, die durch Energie- und Stoffdurchsatz fern vom thermodynamischen Gleichgewicht gehalten wurden. Basierend auf den Arbeiten Alan Turings und Lars Onsagers zeigte er, dass in offenen Systemen, in welchen autokatalytische chemische Reaktionen ablaufen, in der Nähe des thermodynamischen Gleichgewichts zunächst Inhomogenitäten auftreten, die durch Diffusion oder Strömungsprozesse aufrechterhalten werden können. Bei Erreichen eines Übergangspunkt fern vom Gleichgewicht kann das System Symmetriebrüche zeigen, indem es zur Ausbildung einer stationären, geordneten dissipativen Struktur kommt.

 

Chaotic itinerancy (chaotische Wanderschaft) - zwischen Selbstorganisation und Chaos

Ein dynamisches Modell für ein neuronales Netzwerk, das eine Mischung aus Organisation und Chaos darstellt, ist das Modell der "Chaotischen Wanderschaft". Zeitweise werden hier Attraktoren beobachtet, die einen Punktbereich oder eine Zyklus zeigen, und dann werden die Attraktoren wieder zeitweise chaotisch und wandern wild umher.

    Weblink: Chaotic itinerancy online

 

 

3.2 Kohärente Strukturen: Nichtlineare Wellen, Solitonen

• Wandernde Wellen, Schockwellen
• Mehrsolitonen

 

3.3 Musterbildung in Reaktions-Diffusions-Systemen

 

3.3.1 Zweidimensionale Reaktions-Diffusionssysteme: Turing-Strukturen

Bildlizenz-Info: Wikipedia, Public Domain

Das historisch gesehen erste Modell der Morphogenese stammt von Alan Turing und ist als Reaktions-Diffusionsmodell bekannt. In einer zweidimensionalen Ebene können damit Musterbildungsprozesse beschrieben werden, welche aus einem ehemals homogenen Medium emergieren. Es sind sozusagen "Strukturen aus dem Nichts".

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

Das mathematische Modell dazu sieht so aus:

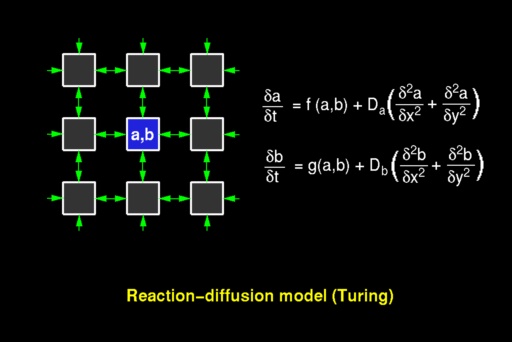
Bildlizenz-Info: Bild erstellt von Przemyslaw Prusinkiewicz, Public Domain online

Jedes Systemelement (Kästchen) wird durch zwei Zahlenwerte a und b charakterisiert, welche die Konzentration zweier Substanzen (Morphogene) repräsentieren. Ein System von gekoppelten partiellen Differentialgleichungen beschreibt dann die Konzentrationsänderungen im Zeitverlauf. Die Substanzen diffundieren dabei auseinander und reagieren währenddessen auch miteinander.

In den Gleichungen werden die Reaktionskomponenten durch die Funktionen f und g beschrieben, und die Diffusionskomponenten durch den übrigen Term. Dieses Modell beschreibt nun den einsetzenden Symmetriebruch und die Aufhebung der Homogenität in einem ursprünglich homogenen Medium.

 

3.3.2 Aktivator-Inhibitor-Modelle

Bildlizenz-Info: Quelle Scholarpedia, Public Domain

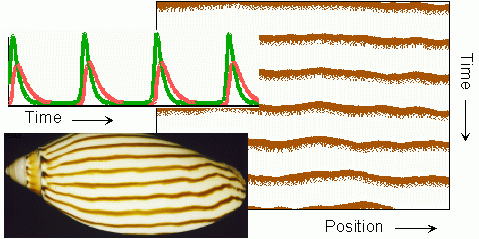
Eine weiter Variante des Reaktions-Diffusionsmodells stellt das Aktivator-Inhibitor-Modell von Gierer und Meinhardt dar. Es wurde benutzt, um die Muster von Muscheln zu modellieren.

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

Im eindimensionalen mathematischen Modell diffundieren die Substrate entlang einer Linie nach folgendem mathematischen Schema:

Bildlizenz-Info: Bild erstellt von Przemyslaw Prusinkiewicz, Public Domain online

Ein Java-Applet zur entsprechenden Musterbildung findet man hier online.

Quasiteilchen in einem Dreikomponentensystem (Purwins)

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

 

3.3.3 Brüsselator

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

Der Brüsselator (benannt nach der Stadt Brüssel) ist das einfachste mathematische Modell, welches chemische Oszillationen darstellen kann, und aufgrund der Nichtlinearität des Gleichungssystems auch stabile Grenzzyklen. Es handelt sich um ein Modell mit zwei Zustandsgrößen (Variablen), und ist daher im Originalmodell grundsätzlich noch nicht chaosfähig.

Chaotisch wird das Modell dann durch Ergänzungen, wie beispielsweise einer periodischen Anregung von Außen ("forced Brusselator"), oder der Kopplung mehrerer Brüsselator-Modelle.

 

3.3.4 Oregonator

Bildldlizenz-Info: Animation selbst erstellt mit  Ready 0.6, Public Domain

Der Oregonator (benannt nach der Stadt Oregon) ist ein im Sinne der Chemiker realistischeres, wenngleich auch komplexeres Modell mit zwei oder drei Zustandsgrößen zur Modellierung von Oszillationen Auch und Grenzzyklen. Trotz der ggf. drei Variablen konnte bislang jedoch keine Entwicklung von Chaos im originalen Modell ohne Erweiterungen nachgewiesen werden.

 

3.3.5 Die  Komplexe Ginzburg-Landau-Gleichung

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

 

 

3.4 Kauffman-Netzwerke (NK-Networks)

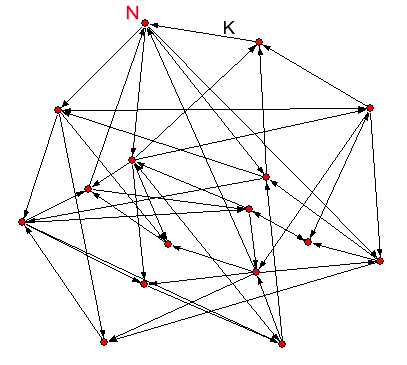
Random Boolean Networks (RBNs)

 

 

3.5 Gekoppelte Abbildungsgitter (CMLs)

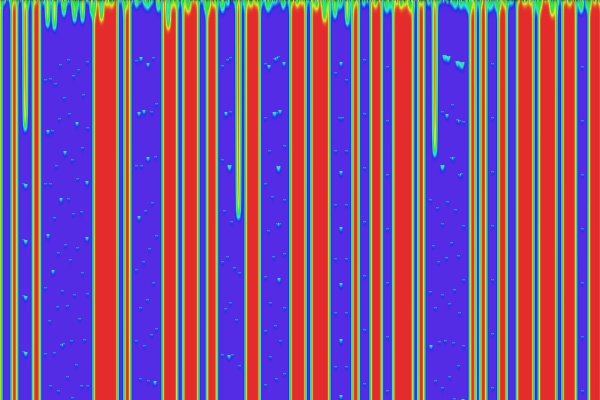
3.5.1 Elementare CMLs

3.5.2 Cellular nonlinear Networks (CNNs)

3.5.3 Diskrete CML's: Zellularautomaten

 

 

3.6 Zellularautomaten

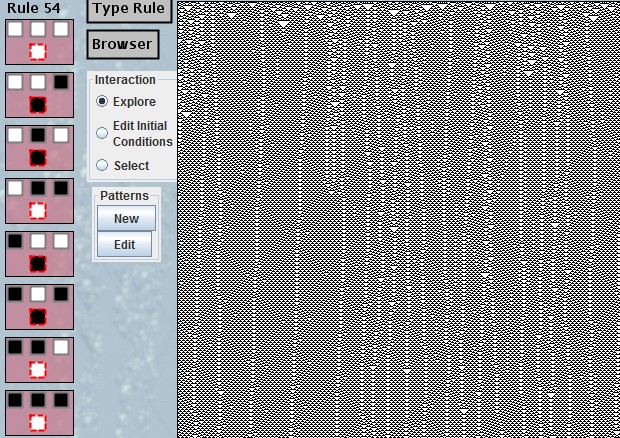
3.6.1 Eindimensionale Zellularautomaten

• Eindimensionale elementare Zellularautomaten
• Eindimensionale totalistische Zellularautomaten
• Eindimensionale Semi-totalistische Zellularautomaten

3.6.2 Zweidimensionale Zellularautomaten

Game of life (Conway), Semi-totalistisch

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

 

Larger than life

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

 

Smooth life

Bildlizenz-Info: Animation selbst erstellt mit Ready 0.6, Public Domain

 

Yin Yang Fire

Analyse

 

 

 

3.7 Zufällige Systemdynamik räumlich ausgedehnter Systeme

Bildlizenz-Info: Animation selbst erstellt mit dem Freeware-Programm "Ready", Version 0.6

Zufallsrauschen

 

Brownsche Bewegung und Langevin-Gleichung

Die Brownsche (Molekular-)Bewegung ist nach dem schottischen Botaniker Robert Brown benannt, der sie 1827 bei seinen Untersuchungen von Pollenkörnern unter dem Lichtmikroskop beobachtete. Er sah eine unregelmäßige Zick-Zack-Bewegung, weswegen er zunächst glaubte, es handle sich bei diesen Bestandteilen der Pollenkörner um Lebewesen. Dass diese Vermutung aber nicht stimmen konnte, zeigten ihm bald weitere Beobachtungen: Auch Ruß- und Staubkörner, ja sogar kleine Metallsplitter bewegten sich. Zudem stellte er fest, dass sich die Teilchen umso heftiger bewegten, je kleiner und damit leichter sie waren. Das heißt, die Geschwindigkeit der Teilchen ist  umso größer, je weniger Masse sie haben.

Die Brownsche Bewegung hat in der Entwicklung der Physik eine wichtige Rolle gespielt, da sie die Idee des Atomismus stützte. Die Erklärung der Brownschen Bewegung wurde erst viel später, nämlich 1905, von Albert Einstein in seinem Aufsatz "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" vorgeschlagen. Er erkannte, dass die Brownsche Bewegung eine Folge der unregelmäßigen Stöße der sich ständig bewegenden Atome und Moleküle ist. Die unter dem Mikroskop sichtbaren Partikel werden ständig von den viel kleineren und daher unsichtbaren Molekülen der Flüssigkeit bzw. des Gases angestoßen und so gewissermaßen "herumgeschubst". Anzahl, Stärke und Richtung der stoßenden Moleküle ändern sich ständig, so dass die beobachtete zufällige Zick-Zack-Bewegung entsteht. 

 

Master-Gleichung

 

Fokker-Planck-Gleichung

 

 

3.8 Die Evolution komplexer dynamischer Netzwerke

Neben der Selbstorganisation von komplexen Systemen, welche stets mit einem Strukturwandel verbunden ist, ist es auch möglich, dass ein System im Laufe einer Evolution sogar seine Identität, d.h. seinen Funktions- und Systemzweck mit der Zeit verändert. Veränderungen dieser Art werden u. a. durch die Möglichkeit der Selbstreproduktion lebender Organismen (Autopoiese) ermöglicht, lassen sich aber auch bei vom Menschen hergestellten Produkten beobachten.

Kennzeichnend für die Evolution ist, das mit der Systemveränderung eine möglicherweise drastische Verschiebung der Systemidentität, also seiner Zielfunktion oder seines Systemzwecks, unter Erhaltung der Systemintegrität einhergeht. Ein evolutionäres Beispiel ist das Entstehen flugfähiger Tiere (Vögel) aus wasserbewohnenden Reptilien.

In der Natur Evolution formt die Evolution aus einfachen Strukturen immer komplexerer Gebilde, wobei sie stets das fortsetzt, was im gegebenen Zeitpunkt funktioniert. Alles Andere wird aussortiert. Komplexe Systeme können für sich genommen bereits ganz erstaunliches leisten. Doch man benötigt die Evolution, damit daraus schließlich auch Systeme werden, die sich flexibel an ihre Umwelt anpassen können.

Die kreativen Fähigkeiten der Evolution, komplexe Gebilde hervorzubringen, sind außerordentlich erstaunlich. Doch man darf nicht vergessen, dass sie dafür auch kosmologische Zeiträume in Anspruch nimmt. Vom Einzeller bis zum Menschen hat sie sich immerhin stolze 3,5 Milliarden Jahre Zeit gelassen. Doch zum Glück besitzen wir heutzutage eine technische Möglichkeit, evolutionäre Vorgänge in einem stark verkürzten Zeitraum per Modell nachzubilden. Die Maschine, die uns dies ermöglicht, ist natürlich der Computer (in dessen Nähe wir uns beim Lesen dieser Zeilen vermutlich auch gerade aufhalten). Computer können Evolutionsvorgänge simulieren und dabei auch spontan Lösungen generieren, die selbst die Programmierer der Software überraschen.

Strukturwissenschaftlich gesehen handelt es sich bei der Evolutionstheorie um die gleichen Phänomene, die auch für komplexe Systeme gelten. Ein paar einfache Regeln und Rückkopplungen reichen, um Komplexität emergieren zu lassen. Eine der einfachen Regeln besagt, dass das untersuchte Objekt in der Lage sein muss, sich selbst zu replizieren, und dabei ein paar zufällige Mutationen und Variationen hervorbringt. Die Rückkopplung findet dann über die Umwelt statt, welche mitbestimmt, welche Objekte die jeweils geeignetsten sind. Selektion ist ein einfacher Feedback-Mechanismus, der hierarchisch verschachtelt und unter bestimmten Randbedingungen zu anscheinend beliebig hoher Komplexität führen kann.

Für die Evolution benötigen wir demnach in Summe alles, was wir über dynamische Systeme wissen. Wir benötigen Morphogenese, eine Zufallsdynamik, lineare Dynamiken (z.B. Schwingungen), nichtlineare Dynamiken, Chaos, Selbstorganisation und die Regeln der Evolution, welche die Veränderlichkeit der Objekte einer Abstammung aller evolutionären Objekte von gemeinsamen Vorfahren beschreibt (Evolution durch Verzweigung), eine fortlaufende Veränderung in allem evolutiven Prozessen sieht, die Vermehrung und die zufällige Mutation als Ursache für das Entstehen von komplexer Vielfalt begreift, und durch den gesteuerten Prozess der Selektion weniger geeignete Lösungsformen schrittweise aus dem Evolutionsprozess entfernt.

Die Evolution als kreativer „Designprozess“ benötigt dabei jedoch keinerlei externen Designer. Sie ist ganz einfach ein inhärentes Potential unseres gesamten Universums per se. Und dies ist auch die interessante Idee, welche letztendlich hinter der spontanen Musterbildung, oder der Selbstorganisation von Systemen steht.

 

 

 

Exkurs: Die BBC-Dokumentation "The secret life of Chaos"

http://topdocumentaryfilms.com/secret-life-chaos/

 

 

 

 

 

Einzelnachweise

^1,2,3  Bossel, Hartmut: Systeme, Dynamik, Simulation; 2004

⁸ siehe Leisen, Josef online

⁹ siehe Sterrer, Roland online