Strukturen der Mathematik
Inhalt
Vorwort: Mathematik als Strukturwissenschaft - die Lehre von abstrakten Strukturen
1. Grundlagen der Mathematik als Strukturwissenschaft
1.1 Sinn und Wahrheitswert mathematischer Aussagen
1.2 Logik als Sprache über eine Struktur
1.3 Mengen - elementare Mengenlehre
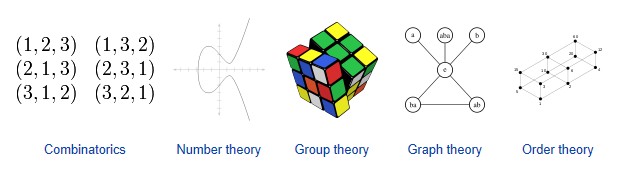
1.4 Kombinatorik, diskrete Mathematik und Graphentheorie
1.5 Elementare Beziehungen: Relationen, Abbildungen (bzw. Funktionen), Konstanten
1.6 Elementarer mathematischer Strukturbegriff
2. Mathematische Strukturen
2.1 Grundstrukturen ("Mutterstrukturen")
2.2 Multiple Strukturen (Mischstrukturen)
2.3 Spezielle Strukturen
3. Spezielle Strukturen I: Netzwerke
3.1 Komplexe Netzwerke
4. Spezielle Strukturen II: Dynamische Systeme und mathematische Evolutionsgleichungen
Vorwort: Mathematik als Lehre von abstrakten Strukturen
Abstrakte Objekte, Mengen, Beziehungen, Strukturen 1
Es gibt eine Vielfalt an grundlegenden Objekten in der Mathematik (Zahlen, Punkte, Funktionen, Mengen ...). Sie sind keine sinnlich erfassbaren Dinge, sondern abstrakte Vorstellungen. Manchmal lassen sich diese Objekte (zumindest in einer Annäherung) visualisieren, zum Beispiel ein geometrisches Gebilde durch eine Zeichnung; man muss sich dann aber darüber im Klaren sein, dass die Zeichnung das Objekt nur abbildet und nicht mit ihm identisch ist.
Auch der Ursprung der mathematischen Objekte kann vielfältig sein: Teils ergeben sie sich als Abstraktionen aus dem Alltag, teils dienen sie der Modellierung, teils dem innermathematischen Verständnis. Mathematische Objekte werden durch ihre Funktionsweise verstanden, also durch ihre Eigenschaften und durch ihr Verhältnis zueinander. Sie werden daher oft auf axiomatische Weise eingeführt: Axiome beschreiben, welche gewünschten Eigenschaften die Objekte haben sollen.
Ob man sinnvollerweise sagen kann, dass solche mathematischen Objekte existieren, und um welche Art von Existenz es sich dann handelt, ist ein philosophisches Problem, um dass sich Mathematiker üblicherweise nicht kümmern. Ihnen reicht es, dass ihre Theorien funktionieren. Dies bedeutet, dass in den Theorien keine Widersprüche auftreten und dass sie geeignet sind, mathematische oder außermathematische Phänomene zu beschreiben.
Da die Widerspruchsfreiheit einer Theorie in der Regel aber nicht bewiesen werden kann, wird üblicherweise erwartet, dass man sie auf eine anerkannte Theorie zurückführt, zumeist auf das mengentheoretische Axiomensystem ZFC. Für mathematische Objekte bedeutet dies, dass man ihre relative Existenz zeigt, d.h. dass man sie zum Beispiel mengentheoretisch modelliert: Man sucht also etwa in der durch ZFC beschriebenen Mengentheorie Objekte, die sich genauso verhalten, wie die Axiome für diese Objekte es vorschreiben. Aufgrund des jahrzehntelangen erfolgreichen Gebrauchs geht man allgemein davon aus, dass die durch ZFC beschriebene Mengenlehre widerspruchsfrei ist, oder zumindest, dass eventuell einmal auftretende Widersprüche nicht den Kern der Mathematik betreffen, sondern durch leichte Veränderungen des Axiomensystems ausgemerzt werden können.
Ebenso wichtig wie die Objekte der Mathematik sind die Bezüge zwischen ihnen. Diese können sich zum Beispiel durch Relationen ausdrücken. So wie etwa die zweistellige Ordnungsrelation auf den natürlichen Zahlen (eine Zahl ist größer als eine andere oder nicht), oder die dreistellige Zwischenrelation auf den Punkten einer Linie (ein Punkt liegt zwischen zwei anderen oder nicht), oder durch die Existenz von Operationen mit gewissen Eigenschaften (z.B. die Addition natürlicher Zahlen), oder durch kompliziertere Verhältnisse. Diese Relationen, Operationen etc. können dann selbst wieder als mathematische Objekte aufgefasst werden.
Eine Menge von Objekten mit gegebenen Bezügen zueinander wird üblicherweise eine Struktur genannt. Ein Großteil der mathematischen Arbeit besteht darin, Strukturen mit bestimmten Eigenschaften zu untersuchen und Sachverhalte darüber zu beweisen (mathematische Sätze oder Theoreme genannt). Insbesondere will man solche Strukturen klassifizieren und finden, die als Modelle für Phänomene aus der Physik, der Wirtschaft etc. dienen können.
Quantität, Struktur, Raum und Veränderung (Quantity, Structure, Space, Change)
Eine weitere interessante Definition zur Gliederung der "Mathematics" schlägt die englische Wikipedia-Website vor (online):
- Quantität (Menge)
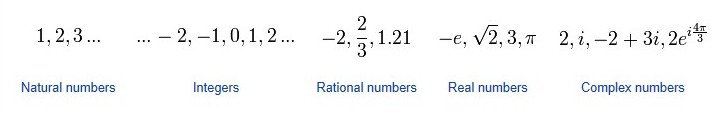
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain - Struktur
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain - (mathematischer) Raum
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain - Veränderung
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain - Erweiterung 1: Angewandte Mathematik
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain - Erweiterung 2: Die Grundlagen der Mathematik (mathematische
Logik, Mengenlehre, Kategorientheorie und die Theorie der
Berechenbarkeit)
Bildlizenz-Info: Wikipedia, Mathematics; Public Domain
Die Klassifikation der American Mathematics Society und die MSC 2010
Die AMS hat mit ihrer Mathematics Subject
Classification folgende Einteilung der Mathematik vorgenommen, die in
erster Line zur Klassifizierung mathematischer Publikationen dient (online):
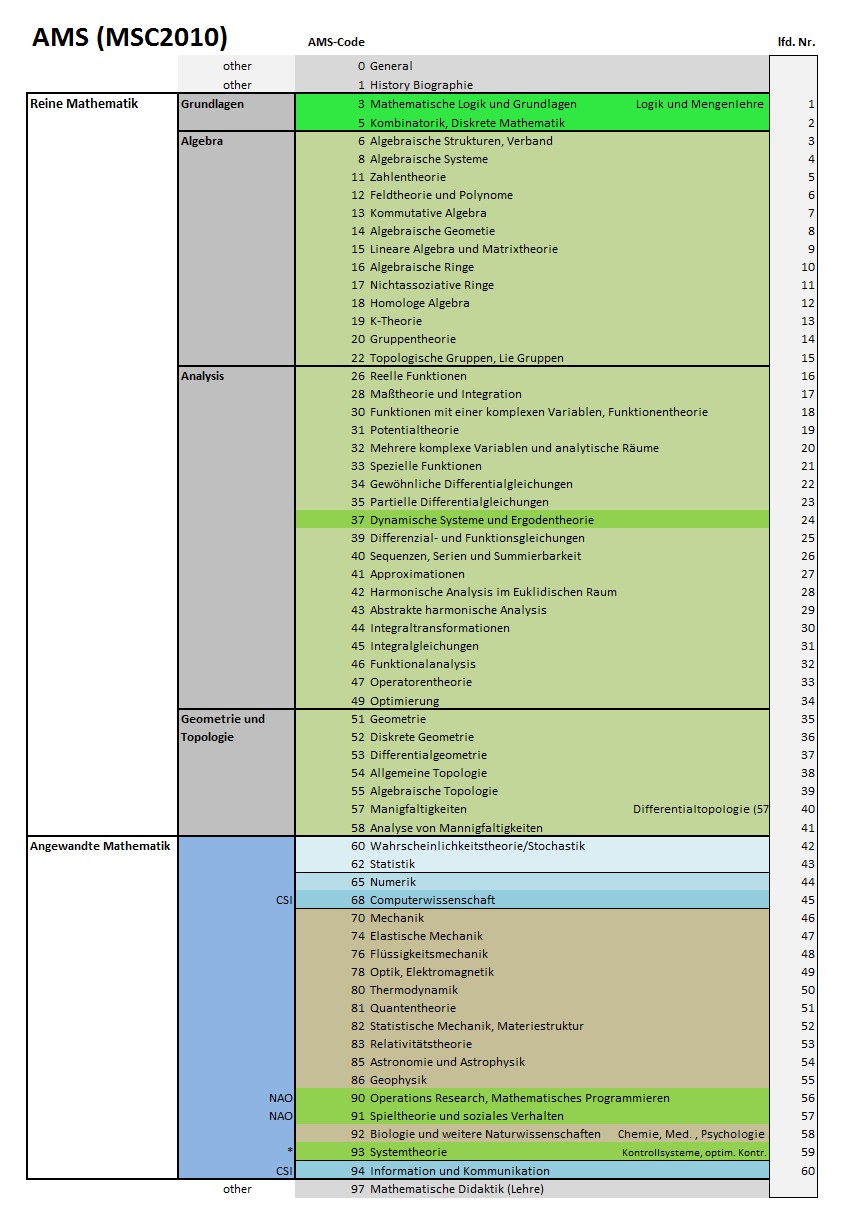
Bildlizenz-Info: Bild selbst erstellt; Public
Domain
Die dargestellte erste Hierarchiestufe enthält rund 60 Kategorien, die zweite Stufe rund 500 und die dritte Gliederungsstufe rund 5000 (!) mathematische Einzeldisziplinen.
Man erhält somit einen ersten Eindruck von der unglaublichen Vielfalt und der Spezialisierung der heutigen Mathematik.
1. Grundlagen der Mathematik als Strukturwissenschaft
1.1 Sinn und der Wahrheitswert von mathematischen Aussagen 2
"Eine Aussage ist ein sprachliches Gebilde, von dem es
sinnvoll ist zu sagen, es sei wahr oder falsch."
Aristoteles
Die Hauptaufgabe eines Mathematikers scheint zunächst darin zu bestehen, Aussagen zu formulieren und sie auf ihren Wahrheitsgehalt zu überprüfen. Doch noch grundlegender ist der Umstand, dass die formulierten Aussagen im mathematischen Sinne sinnvoll sind. Nur sinnvolle Aussagen können überhaupt erst wahr oder falsch sein. So ist etwa die Aussage 1+1=3 keineswegs unsinnig, sondern sinnvoll, wenn auch falsch. Hingegen ist die Aussage 1+=3 nicht sinnvoll, also im eigentlichen Sinne keine Aussage, sondern nur eine bedeutungslose Aneinanderreihung von Symbolen.
Häufig trifft man in der Mathematik auch auf sogenannte unvollständige Aussagen, also sprachliche Gebilde, die erst durch eine geeignete Ergänzung zu einer Aussage werden. So ist beispielsweise die Gleichung x+1=3 weder wahr noch falsch (solange man nicht weiß, was x ist) und daher ebenfalls keine eigentliche Aussage. Erst durch Konkretisierung der Variablen entsteht eine Aussage. Ohne diese Konkretisierung spricht man von einer Aussageform.
Schließlich gibt es auch grammatikalisch vollständige Sätze, die wie sinnvolle Aussagen aussehen, aber trotzdem sinnlos sind, etwa: die Philosophie ist rechteckig. Nicht immer ist die Sinnlosigkeit einer vorgeblichen Aussage so offenkundig wie in diesem Fall. Daher gehen gerade Anfänger der Mathematik darin fehl, dass sie häufig sinnlose und nicht etwa falsche Aussagen formulieren.
1.2 Logik als Sprache über eine Struktur
Strukturen und deren dazugehörige Sprache: Prädikatenlogik
Um über Strukturen eines gegebenen Typs Aussagen machen zu können, benötigen wir eine allgemeine mathematische Sprache L, die aus logischen und nichtlogischen Zeichen besteht.
Logische Zeichen der allgemeinen Sprache:
- Abzählbar unendlich viele Variablen
- Die Junktoren der Aussagelogik ⌐ ˄ ...
- Der Existenzquantor und der Allquantor der Prädikatenlogik
- Das logische Gleichheitszeichen ≡
- Die Klammern ( )
Nichtlogische Zeichen der allgemeinen Sprache:
- Relationszeichen <, =, >, ≤
- Funktionszeichen - + *
- Konstanten 0, 1, ...
Der Typ einer Sprache wird analog zu den Strukturen ebenfalls seine Signatur genannt. Entspricht die Signatur der Sprache dem der Struktur, so wird die allgemeine Sprache L auch als Sprache dieser Struktur genannt, und die Struktur besitzt dann auf der anderen Seite genau diese allgemeine Sprach-Struktur (L-Struktur).
1.3 Mengen - elementare Mengenlehre
Naive Mengenlehre
„Unter einer 'Menge' verstehen wir jede
Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer
Anschauung oder unseres Denkens (welche die 'Elemente' von M genannt
werden) zu einem Ganzen.“
Georg Cantor
Die Mengenlehre ist heutzutage eine unentbehrliche Grundlage für die Strukturierung der Mathematik. Erste Schwierigkeiten mit einer naiven Mengenlehre, die von Cantors Vorstellungen abgeleitet wurden, ergaben sich jedoch, als diese Mengenlehre auch als Basis für die mathematische Logik verwendet werden sollte. Die dabei auftretenden Widersprüche zwangen die Mathematiker zu einer Axiomatisierung der Mengenlehre.
Axiomatische Mengenlehre (ZFC)
Ernst Zermelo entwickelte 1907 die axiomatische Mengenlehre, die er gezielt zur widerspruchsfreien Begründung der Mengenlehre von Cantor und Dedekind schuf. Abraham Fraenkel bemerkte 1921, dass dazu zusätzlich sein Ersetzungsaxiom nötig sei. Zermelo fügte es in sein Zermelo-Fraenkel-System von 1930 ein, das er kurz ZF-System nannte.
Das ZF-System bewährte sich in der Praxis, weshalb es heute als Basis der modernen Mathematik von der Mehrheit der Mathematiker anerkannt ist; keinerlei Widersprüche konnten mehr aus dem ZF-System abgeleitet werden. Die Widerspruchsfreiheit konnte allerdings nur für die Mengenlehre mit endlichen Mengen nachgewiesen werden, aber nicht für das komplette ZF-System, das Cantors Mengenlehre mit unendlichen Mengen enthält. Nach Gödels Unvollständigkeitssatz von 1931 ist ein solcher Nachweis der Widerspruchsfreiheit jedoch prinzipiell nicht möglich.
Fügt man der ZF-Mengenlehre dann noch das Auswahlaxiom C ("Choice") hinzu, erhält man schließlich die axiomatisierte ZFC-Mengenlehre.
1.4 Kombinatorik, diskrete Mathematik und Graphentheorie
Elementare Kombinatorik

Bildlizenz-Info: Wikipedia, abzählende
Kombinatorik; Public Domain

Bildlizenz-Info: Wikipedia, abzählende
Kombinatorik, Public Domain
Permutationen sind Betrachtungen der Anordnungsmöglichkeiten von Objekten.
Bei einer Kombination wird die Reihenfolge der Anordnung außer acht gelassen, bei einer Variation spielt die Anordnung eine Rolle, so dass es immer mehr Variationsmöglichkeiten, als Kombinationsmöglichkeiten gibt.
Graphen und Graphentheorie

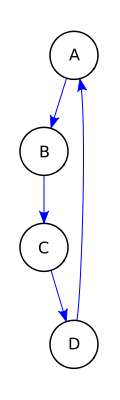
Bildlizenz-Info: Wikipedia, Graphentheorie;
Public Domain
Ein Graph ist ein Tupel aus der Menge der Knoten und der Menge der Kanten. Ungerichtete Graphen (siehe im Bild links) sind Strukturen, in denen die Kantenrelation symmetrisch ist. Gerichtete Graphen werden auch kurz Digraphen genannt.
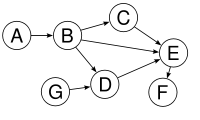
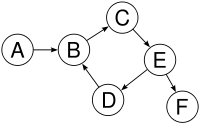
Bildlizenz-Info: Wikipedia, Graph, Public
Domain
Weiterhin unterscheidet man bei den gerichteten Graphen azyklische Graphen ohne Schleifen (im Bild links), die eine Halbordnung bilden, und zyklische Graphen, die Schleifen enthalten und daher keine topologische Halbordnung bilden (also nicht im mathematischen Sinne streng sortierbar sind).
1.5 Beziehungen: Relationen, Abbildungen, Konstanten
Als eine weitere Form von abstrakten Objekten unserer Anschauung finden wir in der Mathematik die verschiedenartigsten Ausprägungen von Beziehungen zwischen den Elementen einer Menge. Man könnte auch etwas salopp sagen, dass die Mathematik (und vielleicht auch das Leben) erst so richtig interessant wird, wenn einzelne Dinge in eine Beziehung miteinander treten.
Was Beziehungen eigentlich ganz genau im mathematischen Sinne sind, davon haben Mathematiker eine ziemlich präzise Vorstellung entwickelt. Sie unterscheiden zur Strukturbildung streng in Relationen, Abbildungen (bzw. Funktionen), und Konstanten. Die folgende Übersicht zeigt den hierarchischen Aufbau der mathematischen Relationen:
Relationen
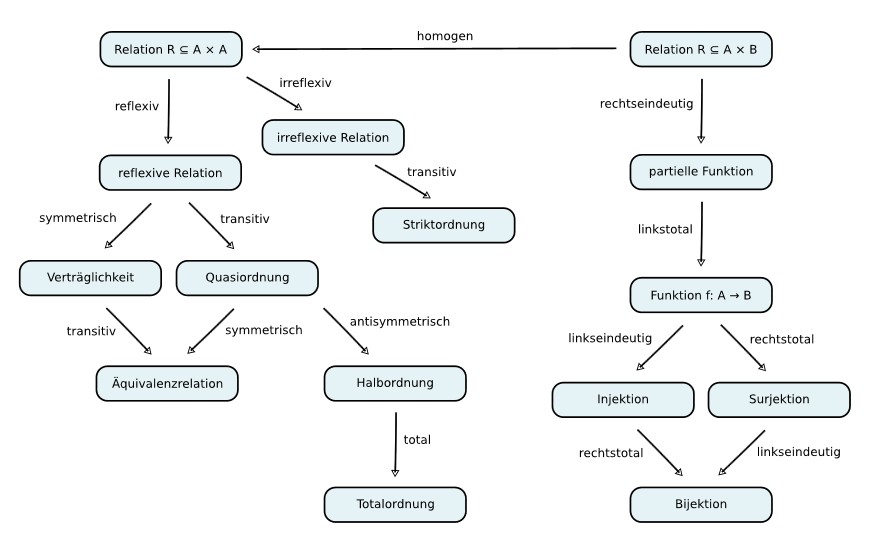
Bildlizenz-Info: Wikipedia (Types of relations
ti.svg), Public Domain
Eine Abbildung bzw. eine Funktion ist dabei eine spezielle Art der Relation zwischen zwei Mengen, bei dem jedem Element der einen Menge genau ein Element der anderen Menge zugeordnet wird. Funktionen nehmen in der Mathematik eine überragende Stellung ein und enthalten als Spezialfälle beispielsweise die Skalar- und Vektorfelder, Transformationen, Operationen, Operatoren (Plus, Minus ...) und Funktoren.
Weiterhin sind in der Mathematik die Ordnungsrelationen (Quasiordnung, Striktordnung, Halbordnung, Totalordnung) und die Äquivalenzrelationen häufig vertreten.
1.4 Elementarer mathematischer Strukturbegriff
Die Idee der mathematischen Struktur
Heutzutage geht man davon aus, dass alle mathematischen Fachgebiete, sofern sie über die Beschäftigung mit der elementaren Mengenlehre, der elementaren Kombinatorik, oder allgemeinen mathematisch-philosophischen Fragestellungen hinaus gehen, sich prinzipiell mit Strukturen beschäftigen.
Die allgemeinste Formulierung einer mathematischen Struktur kommt aus dem Bereich der mathematischen Logik, genauer gesagt der Modelltheorie (siehe auch hier online).
Eine mathematische Struktur besteht als ein 4-Tupel aus
- einer nichtleeren Menge
A als dem Individuenbereich (oder auch
Träger, Domäne oder Universum genannt)
s - ausgezeichneten Relationen auf dem Träger
- ausgezeichneten Funktionen auf dem Träger
- Konstanten des Trägers
Die letzten drei Punkte nennt man auch die Signatur bzw. den Typ einer Struktur. Es handelt sich dabei also um die Anzahl der ausgezeichneten Relationen und Funktionen zusammen mit deren Stelligkeiten sowie der Anzahl der Konstanten.
Eine nullstellige Relation ist als Wahrheitswert definiert. Falls eine Struktur nur nullstellige Relationen enthält, so heißt sie aussagenlogische Interpretation. Eine einstellige Relation ist eine anhand bestimmter Kriterien ausgewählte (segmentierte) Teilmenge einer Menge, oder wird beispielsweise in dem Satz "x ist alt" beschrieben. Einstellige Relationen nennt man auch Eigenschaften. Eine zweistellige Relation ist eine Teilmenge des kartesischen Produkts von zwei Mengen (etwa durch das "Kleiner als"-Symbol <), wie es in dem Satz "x ist älter als y" formulierbar wird, und eine dreistellige Relation drückt beispielsweise der Satz "der x gönnt dem y das z" aus, bis hin zur n-stelligen Relation als Teilmenge des kartesischen Produktes von n Mengen.
Eine nullstellige Funktion ist als Konstante definiert. Eine ein- bis n-stellige Funktion besitzt eine algebraische Struktur. Eine algebraische Struktur, die einstellig ist, benötigt nur ein Argument, wie beispielsweise die Betragsfunktion einer Zahl (der Absolutwert), oder die Vorzeichenumkehr einer Zahl ("mal minus Eins") oder der Kehrwert einer Zahl (Eins geteilt durch eine Zahl). Eine zweistellige funktionale Verknüpfung benötigt zwei Argumente, wie sie beispielsweise bei der Addition, Subtraktion, Multiplikation und Division von mindestens zwei Zahlen auftreten.
- enthält eine Struktur keine Relationen, Funktionen und Konstanten, ist die Struktur eine Menge (quasi eine "Leere Struktur", ähnlich einer leeren Menge)
- enthält eine Struktur Relationen, aber keine Funktionen bzw. Konstanten, spricht man von einer relationalen Struktur
- enthält eine Struktur keine Relationen, aber Funktionen spricht man von einer algebraischen (oder funktionalen) Struktur
Beispiele: Ein gerichteter oder ungerichteter Graph ist eine relationale Struktur, eine Gruppe, die durch eine Verknüpfung von plus/minus gekennzeichnet ist, ist eine algebraische Struktur.
Diese Definition kann zum einen auf mathematische Strukturen, als auch auf die Struktur der Sprache der mathematischen Logik (siehe 1.2) angewandt werden.
2. Mathematische Strukturen 3
2.1 Mathematische Grundstrukturen ("Mutterstrukturen")
Obwohl die Mathematik inzwischen aus über 5000 Einzeldisziplinen (siehe oben beim MSC2010) besteht, gibt es die Idee, ihr Hauptgebäude könne vielleicht auf nur drei basalen Säulen ruhen: der Ordnungsstruktur, der algebraischen Struktur und der topologischen Struktur. Als erstes wurde dieser Versuch eines vereinheitlichten architektonischen Überbaus für einen gemeinsamen Nenner aller mathematischen Objekte und Inhalte von der Mathematiker-Gruppe Bourbaki formuliert. Sie gaben diesen drei Strukturen daher den Namen "Mutterstrukturen (engl. "mother structures").
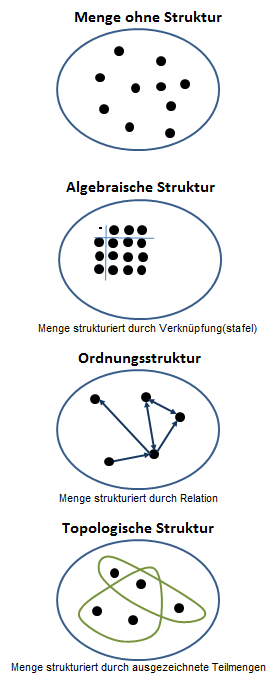
Bildlizenz-Info: Wikimedia (Mathematische
Grundstrukturen.png); Public Domain
Betrachten wir zunächst eine Menge, deren Elemente keine besonderen Eigenschaften haben, und in keinerlei Beziehung zueinander stehen. Diese Menge ist "strukturlos", bzw. kann man sie auch als eine "Nullstruktur" oder "leere Struktur" (ähnlich der leeren Menge, oder der Zahl Null) bezeichnen. Um dieses langweilige Objekt ein wenig interessanter zu gestalten, wird im folgenden dann versucht, ein geordnetes Paar für das System der Menge M versehen mit der Struktur S zu generieren, um der Trägermenge eine Struktur aufzuprägen.
Folgende Einstellung zum Wesen der Mathematik findet hier ihren Niederschlag: Ein fundamentales Konzept in der Mathematik stellen Strukturen dar, die dadurch entstehen, dass Mengen in Verbindung mit dazu gehörigen Relationen und Abbildungen gesehen werden. Derartige Strukturen bilden die Grundlage praktisch aller mathematischen Disziplinen, sobald sie über elementare Mengenlehre, kombinatorische Probleme oder grundlegende mathematisch-philosophische Fragestellungen hinausgehen (siehe auch hier online).
Wichtig zu erwähnen ist auch, dass die Strukturen, insbesondere die Bourbaki-Strukturen, zwar ein zentrales mathematisches Ideengebäude darstellen, aber nicht elementar im mathematischen Sinne sind. Es sind eher basal zusammengesetzte Objekte, so wie es sich beispielsweise auch bei den Atomen der Physik bereits um komplexe Gebilde handelt, die aus noch kleineren Elementarteilchen zusammengesetzt sind. Die Mutterstrukturen wiederum bestehen alle bereits aus Mengen, speziellen Arten von Relationen und speziellen Regeln, wie diese Relationen und Mengen eine Struktur formen.
Strukturen erzeugende Abbildungen - algebraische und topologische Strukturen
Algebraische Strukturen sind Mengen, die durch eine bestimmte Anzahl an ein- oder mehrstelligen inneren und äußeren Verknüpfungen strukturiert sind, was mathematisch auch als Körper bezeichnet wird. Diese Abbildungen (bzw. Funktionen) stellen dann einen Zusammenhang zwischen den Elementen her. Der Prototyp einer solchen Struktur ist die algebraische Gruppe. Sie zeichnen sich beispielsweise durch das Vorhandensein eines neutralen Elements, oder ihre Reversibilität aus, die durch Inversion entsteht.
Eine topologische Struktur bzw. ein Topologischer Raum strukturiert eine Menge durch ein Mengensystem von sogenannten offenen Mengen, also einer Topologie, die durch Umgebungen gekennzeichnet ist. Es kann ebenfalls als eine Art der speziellen mathematischen Abbildung aufgefasst werden. In diesem Fall stehen die Elemente jedoch nicht direkt miteinander in Beziehung, sondern indirekt, zum Beispiel über die gemeinsame Zugehörigkeit zu einer Untermenge. Wichtige Grundbegriffe sind hier die Nachbarschaft, Grenzen und Grenzwertbildungen. Topologische Strukturen sind Mengen, bei denen zu jedem Element eine Menge von Umgebungen existiert.
Strukturen erzeugende Ordnungen - Ordnungsstrukturen
Ordnung ist nicht nur das halbe Leben, sondern auch eine Möglichkeit, Strukturen zu erzeugen. Die Ordnungsstrukturen werden auch Ordnungsrelation genannt und zeigen, wie Elemente miteinander in Beziehung stehen, die in einer bestimmten Anordnung oder Reihenfolge definiert sind. Ein Beispiel in der Natur wäre vielleicht die DNA, welche als Erbgut eine ganze Menge an Informationen in bestimmter Reihenfolge codiert. Die Art der Reversibilität entsteht hier durch die Reziprozität, und nicht durch Inversion oder Negativität, wie bei der algebraischen Struktur.
Kombinationsmöglichkeiten von Grundstrukturen
Es gilt letztendendes also auch für die Mutterstrukturen: Beziehungen zwischen Elementen einer Menge prägen Letzterer eine Struktur auf. Nach Bourbaki besteht jede strukturierte Menge, und sei sie noch so komplex, aus einer Kombination dieser mathematischen Grundstrukturen.
2.2 Multiple Strukturen (Mischstrukturen)
Gemäß dem Bourbaki'schen Aufbau der Mathematik führen die eben genannten Grundstrukturen zu dem multiplen Strukturen (oder auch Mischstrukturen), die unter gewissen Verträglichkeitsbedingungen aus zwei oder allen drei Grundstrukturen zusammengesetzt sind.
Vielfach tragen daher in der Mathematik die untersuchten Mengen mehrere Strukturen: Die Menge der reellen Zahlen ist beispielsweise algebraisch ein Körper, sie ist als Ordnungsstruktur eine lineare Ordnung und topologisch gesehen gehört zu jeder Zahl jedes sie enthaltende Intervall als Umgebung.
Das einfachste Beispiel einer multiplen Struktur ist übrigens die sogenannte topologische Gruppe. Als Trägermenge fungiere die nichtleere Menge M, auf der zwei Strukturen erklärt sind: eine Gruppenstruktur G, wodurch (M, G) eine Gruppe ist, und eine topologische Struktur T, sodass (M, T) die Axiome des topologischen Raums erfüllt. Damit nun aber dadurch "mehr" beziehungsweise "etwas anderes" entsteht, müssen sich die beiden Strukturen in der Menge M vertragen. Strukturen heißen in der Mathematik dann verträglich, wenn beispielsweise bestimmte Stetigkeitsforderungen erfüllt sind. Sind die beiden Strukturen G und T auf der Trägermenge M dann gemäß den Axiomen verträglich, dann heißt (M, G, T) eine topologische Gruppe.
2.3 Spezielle Strukturen (mathematische Einzeldisziplinen und Modelle)
Schließlich erhält man durch Hinzunahme weiterer Axiome die so genannten speziellen Strukturen. Es sind dies sowohl klar umrissene mathematische Einzeldisziplinen als auch kleinere Bereiche, in denen die verschiedensten Modelle untersucht werden.

Bildlizenz-Info: Screenshot vom MSC2010, selbst
erstellt, Public Domain
Werfen wir als Beispiel dazu doch einmal einen Blick in die Klasse 93 der MSC2010-Klassifikation, in der es um die Systemtheorie geht (siehe auch weiter oben). Der Unterpunkt 93B beschäftigt sich dann mit der Kontrollierbarkeit und der Systemstruktur. Und der Unter-Unterpunkt 93B52 handelt schließlich von der Kontrolle per Feedback.
Einerseits ist es daher zwar nicht verwunderlich, dass auch Berufsmathematiker nicht alle der über 5000 Einzeldisziplinen der Mathematik kennen, jedoch überrascht es schon, dass andererseits das Fundament des gesamten mathematischen Gebäudes auf nur drei Grundstrukturen beruht.
3. Spezielle Strukturen I: Netzwerke
Als Netzwerke werden Systeme bezeichnet, deren zugrundeliegende Struktur sich mathematisch als Graph modellieren lässt und die über Mechanismen zu ihrer Organisation verfügen.
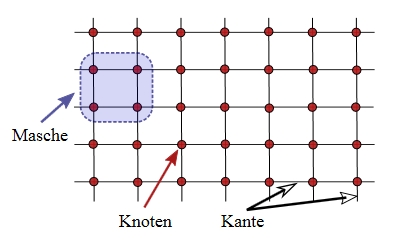
Bildlizenz-Info: Wikipedia, Netzwerk; Public
Domain
Ein Netzwerk besteht aus folgenden Komponenten:
- einer Menge an Elementen, die als Knoten (engl. nodes) bezeichnet werden
- einer Menge an Relationen (Beziehungen), die Kanten genannt werden
- ein geschlossener Zug aus Kanten und Knoten heißt Masche
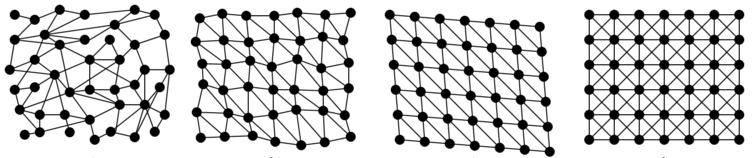
Bildlizenz-Info: Wikipedia, Polygonnetz; Public
Domain
Netzwerke finden sowohl in der Naturwissenschaft, als auch in der Strukturwissenschaft ein weites Anwendungsfeld. Beispielsweise als Koordinatennetz, bzw. Koordinatensystem, oder als oben abgebildetes Polygonnetz (mit von links nach recht zunehmender Regelmäßigkeit).
Es gibt folgende Netzwerkarten:
- Kettennetzwerk (Daisy Chain), lineare Aneinanderreihung
- Sternnetzwerk
- Baumartiges Netzwerk
- All-to-All Netzwerk (full Graph), jeder Knoten ist mit jedem Anderen verbunden
Eigenschaften von Netzwerken:
- Relationsstärke (Beziehungsstärke)
- Netzwerkdichte (Verhältnis von vorhandenen Kanten zur maximal möglichen Kantenanzahl)
- Netzwerkreichweite
- Clusterkoeffizient (Wahrscheinlichkeit, dass bei drei Knoten, die bereits zwei Kanten besitzen, noch eine dritte Kante existiert)
3.1 Komplexe Netzwerke4
Ein komplexes Netzwerk ist im Rahmen der Netzwerkforschung ein Netzwerk mit u. a. nicht-trivialen topologischen Eigenschaften.
Komplexe Netzwerke sind dabei weder als Zufallsnetzwerk, noch als vollkommen reguläre Gitter realisiert, sondern liegen irgendwo dazwischen.
Im Rahmen der aktuellen Forschung untersucht man sowohl komplexe Dynamiken in komplexen Netzwerken, wie beispielsweise Selbstorganisationseffekte, Synchronisation, oder kritisches Verhalten. Weiterhin erforscht man auch sich zeitlich verändernde Netzwerke, bei denen im Laufe der Zeit Knoten und Kanten hinzugefügt, oder entfernt werden (evolutionäre Netzwerke).
Mathematische Analysemethoden umfassen:
- degree centrality (Knotenzentralität, Knotengrad)
- closeness centrality (Knotennähe)
- betweenness centrality
- eigenvector centrality
4. Spezielle Strukturen II: Dynamische Systeme und mathematische Evolutionsgleichungen
Dynamische Systeme und Numerik
An die aktuelle Mathematik der Natur- und Ingenieurswissenschaften werden Fragen von großer Komplexität gestellt, die nur durch das Ineinandergreifen unterschiedlicher mathematischer Gebiete in Angriff genommen werden können. Auch werden die Methoden der reinen und angewandten Mathematik immer stärker zusammengeführt. Bei den dynamischen Systemen sind dies vor allem die Funktionalanalysis und die Numerische Analysis.
Die gesamte moderne Analysis beruht heute auf der Funktionalanalysis. Sie stellt als elegante mathematische Theorie allgemeine Hilfsmittel bereit, um mathematische Aufgabenstellungen, wie gewöhnliche und partielle Differenzialgleichungen, Integralgleichungen und Extremalprobleme in übersichtlicher und einheitlicher Weise zu lösen.
Eine im Rahmen der modernen Mathematik der dynamischen Systeme wichtig gewordene Eigenschaft ist die Lösungsbifurkation von Differentialgleichungen. Die analytische Bifurkationstheorie kann als Brücke zwischen der elementaren Theorie gewöhnlicher Differenzialgleichungen und den Anfängen der so genannten nichtlinearen Dynamik verstanden werden.
Wegen der Nichtlinearität der mathematischen Modelle können dynamische Systeme aus der Praxis ohne leistungsfähige numerische Verfahren zukünftig nicht erfolgreich analysiert werden. Deshalb sind Naturwissenschaftler und Ingenieure auf effiziente Algorithmen und Computer bei der Erforschung der Modelle ihres Fachgebietes angewiesen. Für umfangreiche Computersimulationen realer Prozesse werden schnelle und zuverlässige numerische Verfahren benötigt, deren grundlegendes Verständnis und Einordnung in zunehmendem Maße Bestandteil der mathematischen Ausbildung werden wird. Das Wissenschaftliche Rechnen (Scientific Computing) in Mathematik, Natur- und Ingenieurwissenschaften nutzt effiziente analytische und numerische Verfahren besonders für nichtlineare und großdimensionale Probleme.
Nichtlineare Randwertprobleme
Ein weiteres interessantes Gebiet bei der strukturwissenschaftlichen Erforschung im Bereich der dynamischen Systemen gilt den nichtlinearen Randwertproblemen, insbesondere für elliptische partielle Differentialgleichungen. Die Lösungen solcher Probleme beschreiben, grob gesprochen, die Formen der Gleichgewichtszustände nichtlinearer Systeme, und derartige Situationen kommen überall in Physik und Technik sowie auch in der Biologie vor. Die Methoden zur Behandlung dieser Probleme sind vielfältig, und es herrscht eine rege Wechselwirkung zwischen den Methoden, die speziell auf gewöhnliche Differentialgleichungen anwendbar sind, und den eigens für partielle Differentialgleichungen entwickelten Techniken.
Zum Einsatz kommen dabei beispielsweise Methoden, die der Funktionalanalysis und der Variationsrechnung entstammen, und auch die algebraische Topologie spielt mit hinein, denn die Lösbarkeit einer Gleichung erweist sich häufig als äquivalent zur Nichtexistenz einer Deformation, die gerade aufgrund topologischer Gegebenheiten unmöglich existieren kann. Von besonderem Interesse ist dann die Frage, wie die Lösungsmenge von etwaigen Parametern abhängt, und insbesondere, wo die sog. Verzweigungspunkte liegen, d. h. diejenigen Parameterwerte, bei denen sich die Lösungsmenge sprunghaft ändert.
Evolutionsgleichungen
Evolutionsgleichungen sind Gleichungen, in denen eine Variable die Zeit ist. Evolutionsgleichungen treten daher überall in der Physik, der Biologie oder den Wirtschaftswissenschaften auf, wenn zeitabhängige Prozesse beschrieben werden sollen. Beispiele von Evolutionsgleichungen sind die Black-Scholes Gleichung, die Wellengleichung oder Populationsgleichungen.
Die mathematische Theorie, die uns hilft, Evolutionsgleichungen zu studieren, ist die Theorie der Operatorhalbgruppen. Für solche Operatorhalbgruppen gibt es eine recht vollständige Theorie, mit deren Hilfe man die Eigenschaften des zugrundeliegenden dynamischen Systems untersuchen kann. Dieser Zugang beruht wesentlich auf funktionalanalytischen Denkweisen und Resultaten.
Einzelnachweise
1 Junker, Markus: Einführung in Sprache und Grundbegriffe der Mathematik; 2010, S.2 online
2 Grudzinski, Olaf: Mathematische Grundlagen; 2002, S.6 online3 Basieux, Pierre: Die Architektur der Mathematik - Denken in Strukturen; 2000
4 Wikipedia: Komplexes Netzwerk; 2014