Komplexe Strukturen der Systemwissenschaften
Die logistische Gleichung und die eindimensionale Diskretisierung von Chaos
Am Anfang der logistischen Gleichung standen die Untersuchungen von Robert May über Tierpopulationen. Doch die logistische Gleichung ist zunächst nur eindimensional.
Sehen wir uns dazu die entsprechende Formel einmal an:
xn+1 = µ * xn * (1 - xn), bzw. xn+1 = µ * (xn - xn2), oder auch xn+1 = µxn - µxn2
Mathematisch betrachtet erkennen wir an der Quadrierung von xn die Nichtlinearität, µ nennt man den fixen Kontrollparameter und x ist die einzige variable Größe, daher ist die Gleichung auf den ersten Blick lediglich eindimensional.
Das die logistische Gleichung eine Diskretisierung des Systemverhaltens auf eine eindimensionale Gleichung darstellt, ist ziemlich trickreich, denn sie stellt eigentlich genau genommen eine Datenreduktion um mehrere Dimensionen dar, wenn man so will. Die logistische Gleichung als Rückabbildung entsteht nämlich über eine erste Datenreduktion um eine Dimension, den Poincaré-Schnitt. Aus dem Poincaré-Schnitt kann man wiederum in einem zweiten Schritt eine Iterationsfunktion bekommen, ohne dass Information über das Langzeitverhalten verloren geht. Chaos braucht eine Mindestfreiheit, nämlich drei Freiheitsgrade. Und auch das von Robert May untersuchte Ökosystem hat mehr Freiheitsgrade als nur einen.
Doch wie sieht nun eigentlich genau das unerwartet interessante und abwechslungsreiche Verhalten dieser cleveren "einfachen" Formel aus?
Mit µ von 0 bis 1 (in der Abbildung ist µ=0,82) geht der Grenzwert gegen Null. Es kommt somit immer zu einer Auslöschung (negatives Wachstum). Dieses Verhalten entspricht somit einem Punktattraktor:
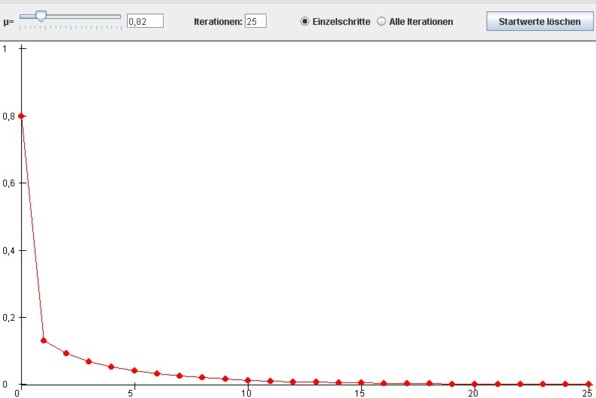
Bildlizenz-Info: Bild selbst erstellt
Mit µ zwischen 1 bis 2 (in der Abbildung ist µ=1,65) stellt sich ein Grenzwert ein. Die Annäherung an den Grenzwert erfolgt monoton. Dies ist ebenfalls ein Punktattraktor:
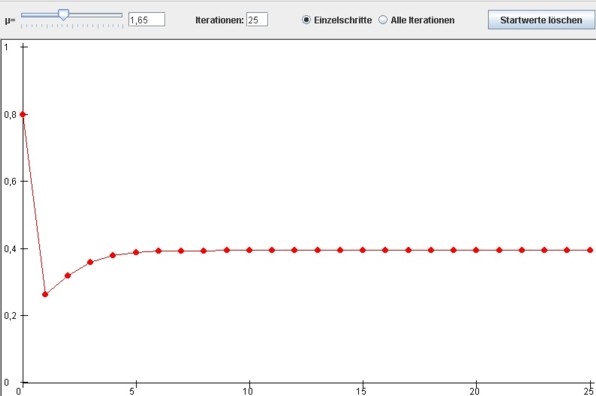
Bildlizenz-Info: Bild selbst erstellt
Mit µ zwischen 2 und 3 nähert sich die Population ihrem Grenzwert wellenförmig, d. h. die Werte liegen ab einem bestimmten n abwechselnd über und unter dem Grenzwert. Hier spricht man von Oszillation um einen Punktattraktor:
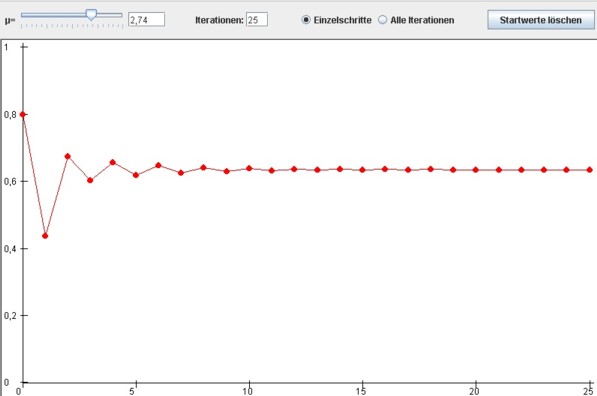
Bildlizenz-Info: Bild selbst erstellt
Mit µ zwischen 3 und etwa 3,45 wechselt die Folge bei fast allen
Startwerten.
Hier spricht man von einem Zyklusattraktor mit
2-periodischen Zyklen:
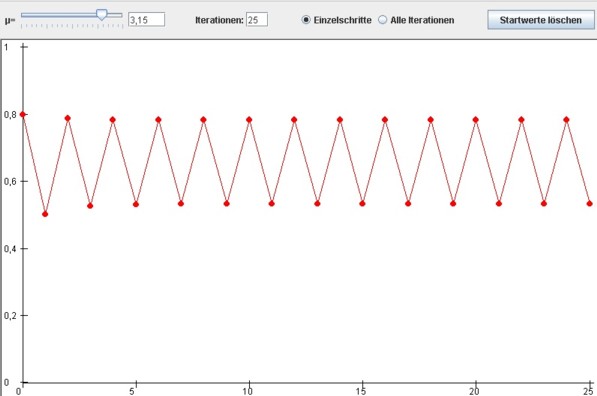
Bildlizenz-Info: Bild selbst erstellt
Mit µ zwischen 3,45 und ungefähr 3,56 wechselt die Folge bei fast allen Startwerten zwischen den Umgebungen von vier bis 16 Häufungspunkten. Man spricht dabei von 4, 8, 16 usw. -periodischen Zyklen:
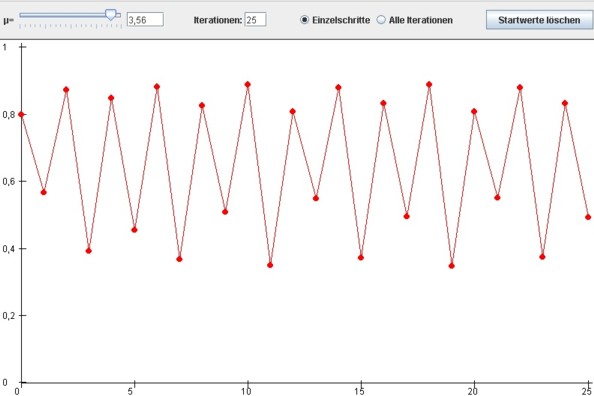
Bildlizenz-Info: Bild selbst erstellt
Bei µ annähernd 3,57 beginnt das Chaos: Perioden sind nicht mehr
erkennbar, winzige Änderungen des Anfangswertes resultieren in
unterschiedlichsten Folgewerten - eine typische Eigenschaft des Chaos.
Man spricht auch von nichtperiodischen Zyklen:
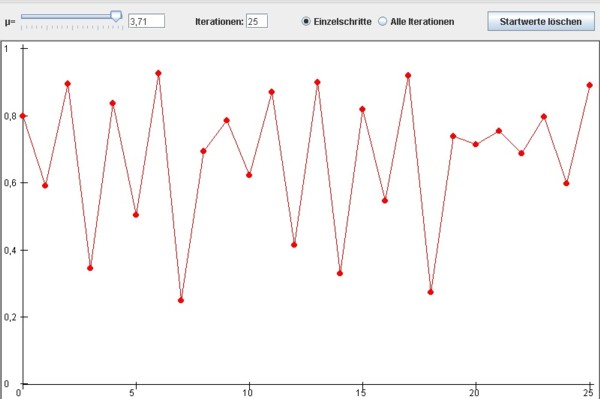
Bildlizenz-Info: Bild selbst erstellt
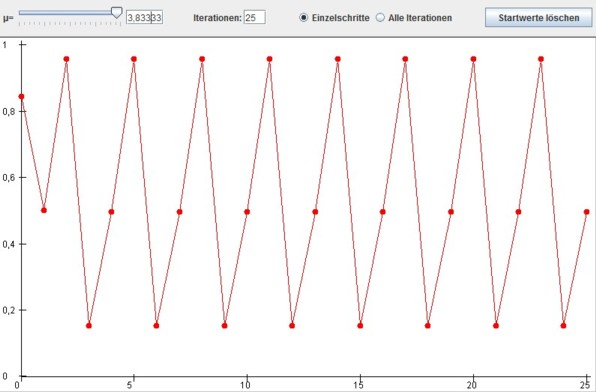
Die Bereiche zwischen
Ordnung und Chaos können sich abwechseln. Es gibt dabei so etwas wie die
"Inseln in Chaos".
Man spricht in diesem Zusammenhang von Intermittenz
(hier durch einen
3-periodischen Zykel):
:
Bildlizenz-Info: Bild selbst erstellt
Intermittenz bedeutet konkret, dass irreguläre Bewegungsabläufe durch reguläre Bewegungsabläufe unterbrochen werden. Intermittenz ist eine Art Erinnerungsvermögen in nicht-linearen Systemen, eine Erinnerung an nicht-chaotische Attraktoren. Intermittenz ist keineswegs eine Seltenheit in nicht-linearen dynamischen Systemen und legt die Vermutung nahe, das Ordnung und Unordnung beides Merkmale von ein und demselben Prozess in einem komplexen System darstellen.
Oberhalb von µ = 3,83 bricht wieder das chaotische Verhalten aus:
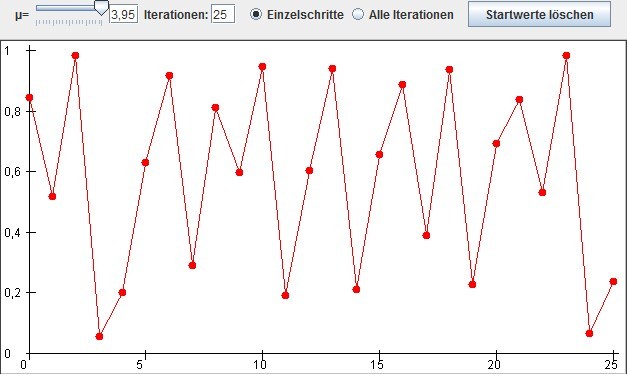
Bildlizenz-Info: Bild selbst erstellt
Einzelnachweise
siehe Leisen, Josef online